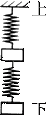题目内容
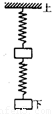
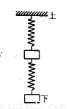
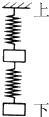 Sl和S2表示劲度系数分别为kl和k2的两根弹簧,k1>k2;a和b表示质量分别为ma和mb 的两个小物块,ma>mb.将弹簧与物块按图示方式悬挂起来.若当S1、S2、a、b适当放置时,两弹簧的总长度最大,在图中标出S1、S2、a、b并求这时两根弹簧的形变量之和(重力加速度为g).
Sl和S2表示劲度系数分别为kl和k2的两根弹簧,k1>k2;a和b表示质量分别为ma和mb 的两个小物块,ma>mb.将弹簧与物块按图示方式悬挂起来.若当S1、S2、a、b适当放置时,两弹簧的总长度最大,在图中标出S1、S2、a、b并求这时两根弹簧的形变量之和(重力加速度为g).分析:相等的拉力作用下,弹簧的劲度系数越小,伸长量越大;对同一个弹簧,拉力越大,伸长量越大;整体法受力分析根据胡克定律求上面弹簧的长,然后隔离法对ma受力分析根据胡克定律求下面弹簧的长度
解答:解:相等的拉力作用下,弹簧的劲度系数越小,伸长量越大;所以需要把劲度系数较小的S2 放在上面;对同一个弹簧,拉力越大,伸长量越大;所以,要想使放在下面的弹簧伸长量大一些,需要把较大质量的小物块a放在下面.如图:

以m1m2整体为研究对象进行受力分析,根据平衡条件有:k2△x1=mag+mbg ①
以m2为研究对象,有:mag=k1△x2 ②
两弹簧的总形变量△x=△x1+△x2 ③
联立①②③得:△x=
答:这时两根弹簧的形变量之和

以m1m2整体为研究对象进行受力分析,根据平衡条件有:k2△x1=mag+mbg ①
以m2为研究对象,有:mag=k1△x2 ②
两弹簧的总形变量△x=△x1+△x2 ③
联立①②③得:△x=
| k1(ma+mb)g+k2mag |
| k1k2 |
答:这时两根弹簧的形变量之和
| k1(ma+mb)g+k2mag |
| k1k2 |
点评:本题的关键是当两弹簧的总形变量等于下面弹簧的伸长量与上面弹簧的伸长量之和.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
如图,Sl和S2表示劲度系数分别为kl和k2的两根弹簧,k1 >k2;a和b表示质量分别为m1和m2 的两个小物块,m1>m2.将弹簧与物块按图示方式悬挂起来。现要求两根弹簧的总长度最大,则应使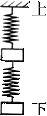
| A.S1在上,a在上 |
| B.S1在上,b在上 |
| C.S2在上,a在上 |
| D.S2在上,b在上 |