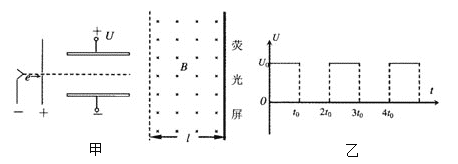
题目内容
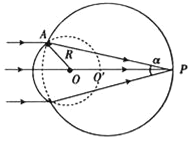
【题目】某透明体外形如图所示，它由折射率相同、半径不同的两个共轴球体组成，大球外表面镀了一层不透光物质，且大球的球心O′恰好在小球球面上，平行轴线的光束从半径为R的小球射入，会聚在轴线上的P点，光线的会聚角α=30°，真空中光速为c．求：（答案可以用三角函数表示）
①透明体的折射率；
②从两球体的交点处射入的光线，从进入透明体至到达P点的时间．
【答案】①
；②
【解析】①连接AO′，由几何关系知，折射角 r=∠OAO′+∠O′AP=45°
入射角 i=∠OAO′+∠AO′O=60
由折射定律有 n=
解得透明体的折射率 n=
；
②由几何关系可知大球半径 R′=2Rcos30°=
R
光线在球中的传播距离 L=2R′cos15°=2Rcos15°
光在球内传播速度 v=
=
则所示时间为 t=
=
练习册系列答案
阅读快车系列答案
相关题目
【题目】某同学描绘小灯泡的伏安特性曲线，实验器材有：
电压表：量程为3V，内阻为3kΩ
电流表；量程为0.6A，内阻约为2Ω
定值电阻R0；阻值为1kΩ
小灯泡L：额定电压为3.8 V
滑动变阻器R：阻值范围为010Ω
电池E：电动势为6V
开关S，导线若干．
该同学按如图甲所示的电路图进行实验，通过正确实验操作和读数，得到了一组电压表的示数和电流表的示数，部分数据如下表：
电流（A） | 0.085 | 0.155 | 0.212 | 0.235 | 0.278 | 0.315 |
电压（V） | 0.17 | 0.60 | 1.20 | 1.50 | 2.10 | 2.70 |
（1）当电压表示数为1.20 V时，小灯泡两端的电压为__V．（保留三位有效数字）
（2）在图乙中画出小灯泡的伏安特性曲线_______．
（3）若把这个小灯泡与电动势为3V、内阻为10Ω的干电池连接成闭合电路，此时小灯泡的电阻为__Ω，实际功率为__W．（结果保留两位有效数字）
