题目内容
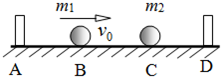 如图所示,两个不计厚度的弹性挡板分别固定在水平桌面上A、D的位置,两个大小相同可看作质点的小球质量分别为m1、m2,且m2=5m1,开始时两球位于B、C的位置,且AB=BC=CD=L,m2静止,m1以水平初速度v0向m2运动,设两球之间、球与挡板之间的碰撞均没有机械能损失,碰撞时间、所有摩擦均不计.求
如图所示,两个不计厚度的弹性挡板分别固定在水平桌面上A、D的位置,两个大小相同可看作质点的小球质量分别为m1、m2,且m2=5m1,开始时两球位于B、C的位置,且AB=BC=CD=L,m2静止,m1以水平初速度v0向m2运动,设两球之间、球与挡板之间的碰撞均没有机械能损失,碰撞时间、所有摩擦均不计.求(1)m1和m2之间发生第一次碰撞后各自的速度大小
(2)经过多长时间两球均回到起始状态.
分析:(1)由题意知,两球之间的碰撞没有机械能损失,遵守动量守恒和机械能守恒,由两大守恒定律列式求解m1和m2之间发生第一次碰撞后各自的速度大小.
(2)碰后m2运动到D位置时,与挡板相碰,以原速率弹回,由运动学公式可求出m2从C点碰后第一次返回C位置所用的时间.同理可求出m1从C点碰后第一次返回C位置所用的时间,结果两球在C位置第二次相碰.m1,m2第二次碰撞过程是它们在C位置第一次相碰的逆过程,即碰后m2停在C位置,m1又以v0的速度水平向左运动.再根据运动学公式求出m1从第二次碰后到下一次以水平向右的速度返回B点所用时间,以及m1第一次碰前从B到C所用时间,即可得解.
(2)碰后m2运动到D位置时,与挡板相碰,以原速率弹回,由运动学公式可求出m2从C点碰后第一次返回C位置所用的时间.同理可求出m1从C点碰后第一次返回C位置所用的时间,结果两球在C位置第二次相碰.m1,m2第二次碰撞过程是它们在C位置第一次相碰的逆过程,即碰后m2停在C位置,m1又以v0的速度水平向左运动.再根据运动学公式求出m1从第二次碰后到下一次以水平向右的速度返回B点所用时间,以及m1第一次碰前从B到C所用时间,即可得解.
解答:解:(1)令v1、v2分别表示m1与m2第一次碰后两球的速度,规定碰前m1的速度v0的方向为正方向.
对m1、m2所构成的系统,由动量守恒定律和机械能守恒定律,得:
m1v0=m1v1+m2v2
m1
=
m1
+
m2
结合题目情景解得:v1=-
v0 v2=
v0
(2)碰后m2运动到D位置时,与挡板相碰,以原速率弹回,
m2从C点碰后第一次返回C位置所用时间:t2=
=
同理,m1从C点碰后第一次返回C位置所用时间:t2′=
=
故m2与m1将在C位置第二次相碰.
m1,m2第二次碰撞过程是它们在C位置第一次相碰的逆过程,即碰后m2停在C位置,m1又以v0的速度水平向左运动.
或:令v1′、v2′分别表示m1与m2第二次碰后两球的速度,对m1,m2所构成的系统,仍以v0的方向为正方向,由动量守恒定律和机械能守恒定律,得:
m1(-v1)+m2(-v2)=m1 v1′+m2 v2′
m1
+
m2
=
m1
+
m2
结合题目情景解得:v1′=-v0 v2′=0
m1从第二次碰后到下一次以水平向右的速度返回B点所用时间为:t3=
m1第一次碰前从B到C所用时间为:t1=
设经过时间T两球均回到起始状态,则有:T=t1+t2+t3=
答:(1)m1和m2之间发生第一次碰撞后各自的速度大小分别为
v0和
v0.
(2)经过
时间两球均回到起始状态.
对m1、m2所构成的系统,由动量守恒定律和机械能守恒定律,得:
m1v0=m1v1+m2v2
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
结合题目情景解得:v1=-
| 2 |
| 3 |
| 1 |
| 3 |
(2)碰后m2运动到D位置时,与挡板相碰,以原速率弹回,
m2从C点碰后第一次返回C位置所用时间:t2=
| 2L | ||
|
| 6L |
| v0 |
同理,m1从C点碰后第一次返回C位置所用时间:t2′=
| 4L | ||
|
| 6L |
| v0 |
故m2与m1将在C位置第二次相碰.
m1,m2第二次碰撞过程是它们在C位置第一次相碰的逆过程,即碰后m2停在C位置,m1又以v0的速度水平向左运动.
或:令v1′、v2′分别表示m1与m2第二次碰后两球的速度,对m1,m2所构成的系统,仍以v0的方向为正方向,由动量守恒定律和机械能守恒定律,得:
m1(-v1)+m2(-v2)=m1 v1′+m2 v2′
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v′ | 2 1 |
| 1 |
| 2 |
| v′ | 2 2 |
结合题目情景解得:v1′=-v0 v2′=0
m1从第二次碰后到下一次以水平向右的速度返回B点所用时间为:t3=
| 3L |
| v0 |
m1第一次碰前从B到C所用时间为:t1=
| L |
| v0 |
设经过时间T两球均回到起始状态,则有:T=t1+t2+t3=
| 10L |
| v0 |
答:(1)m1和m2之间发生第一次碰撞后各自的速度大小分别为
| 2 |
| 3 |
| 1 |
| 3 |
(2)经过
| 10L |
| v0 |
点评:本题是弹性碰撞与匀速运动结合的问题,根据动量守恒、机械能守恒和匀速运动速度公式结合进行求解.

练习册系列答案
相关题目
弦乐器小提琴是由两端固定的琴弦产生振动而发音的,如图甲所示,为了研究同一根琴弦振动频率与哪些因素有关,可利用图乙所示的实验装置,一块厚木板上有AB两个楔支撑着琴弦,其中A楔固定,B楔可沿木板移动来改变琴弦振动部分的长度,将琴弦的末端固定在木板O点,另一端通过滑轮接上砝码以提供一定拉力,轻轻拨动琴弦,在AB间产生振动.(不计摩擦)
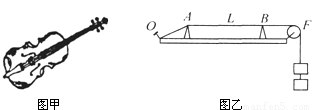
(1)先保持拉力为150N不变,改变AB的距离L(即改变琴弦长度),测出不同长度时琴弦振动的频率,记录结果如表1所示.
表1
从表1数据可判断在拉力不变时,琴弦振动的频率f与弦长L的关系为 .
(2)保持琴弦长度为0.80m不变,改变拉力,测出不同拉力时琴弦振动的频率,记录结果如表2所示.
表2
从表2数据可判断在琴弦长度不变时,琴弦振动的频率f与拉力F的关系为 .
(3)综合上述两项测试可知当这根琴弦的长为0.75m,拉力为225N时,它的频率是 Hz(精确到个位数).

(1)先保持拉力为150N不变,改变AB的距离L(即改变琴弦长度),测出不同长度时琴弦振动的频率,记录结果如表1所示.
表1
| 长度大小L/m | 1.00 | 0.85 | 0.70 | 0.55 | 0.40 |
| 振动频率f/Hz | 150 | 176 | 214 | 273 | 375 |
(2)保持琴弦长度为0.80m不变,改变拉力,测出不同拉力时琴弦振动的频率,记录结果如表2所示.
表2
| 拉力大小F/N | 360 | 300 | 240 | 180 | 120 |
| 振动频率f/Hz | 290 | 265 | 237 | 205 | 168 |
(3)综合上述两项测试可知当这根琴弦的长为0.75m,拉力为225N时,它的频率是 Hz(精确到个位数).