题目内容
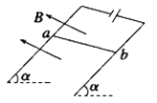
【题目】如图甲所示，AB是以恒定速度v0顺时针传动的水平传送带，CD是以v=5m/s的恒定速度顺时针传动的倾斜传送带、其倾角θ=30°，倾斜传送带两端点C、D的高度差h=lm，C点与水平传送带在同一水平面，两传送带通过一段光滑的水平面相连。现将一质量m1=1kg的物块a(可视为质点)在A处放到水平传送带上，放置时初速度为零，经2s运送到水平传送带的最右端B处，从物块a放到水平传送带上开始计时，其速度－时间图象如图乙所示，物块a离开水平传送带之后与水平面上静止的另一质量m2=2g物块b(可视为质点)发生弹性碰撞，碰后物块b向右运动一小段距离后滑上倾斜传送带。已知两传送带均由不同的电动机带动，传送带与轮子间尤相对滑动，不计轮轴处的摩擦，两物块与倾斜传送带之间的动摩擦因数均为
，忽略两物块在水平面与传送带之间转移时的能量损失，重力加速度g取10m/s2，求：
(1)两物块在水平面上碰撞后的速度大小分别是多少；
(2)由于传送物块b，带动倾斜传送带的电动机多消耗的电能；
(3)物块a与水平传送带因摩擦所产生的热量为多少。
【答案】（1）
，
（2）32J （3）42J
【解析】
（1）两物块在碰撞过程中，动量守恒且机械能守恒，列出表达式可求解两物块在水平面上碰撞后的速度大小；
（2）由于传送物块b，带动倾斜传送带的电动机多消耗的电能等于倾斜传送带克服摩擦力所做的功；
（3）求解物块在水平传送带上运动时相对传送带的位移，然后根据Q=fx相对求解热量；
（1）取向右为正方向，设两物块在水平面上碰撞后物块a的速度v1，物块b的速度为v2，由题可知，物块a碰前的速度为v0=5m/s，物块a与物块b碰撞时满足：
解得：v1=-2m/s，v2=4m/s
（2）由牛顿第二定律可知，物块b在倾斜传送带上运动时的加速度大小为a=μgcosθ-gsinθ=2.5m/s2
物块b加速到5m/s的过程中行驶的位移满足2ax=v2-v22
解得x=1.8m<
此过程中倾斜传送带运动的位移
物块b会继续向上匀速运动x2=0.2m
此时摩擦力为静摩擦力Ff=m2gsin300=10N
由于传送物块b,带动倾斜传送带的电动机多消耗的电能等于倾斜传送带克服摩擦力所做的功，即
（3）物块a运动的速度-时间图像可知：水平传送带的速度v0=6m/s，
加速时间t1=1.2s，加速度大小a1=5m/s，物块a与水平传送带间的滑动摩擦力Ff1=m1a1=5N；物块a第一次在水平传送带向右运动时，
两者的相对位移
碰撞后物块a向左运动，在传送带上向左减速的时间
此过程中两者的相对位移
然后向右滑离水平传送带沿倾斜传送带运动，所以物块a与水平传送带因摩擦产生的热量为：
