题目内容
如下图(a)所示,木板OA可绕轴O在竖直平面内转动,某研究小组利用此装置探索物块在方向始终平行于斜面、大小为F=8N的力作用下加速度与斜面倾角的关系.已知物块的质量m=1kg,通过DIS实验,得到如图(b)所示的加速度与斜面倾角的关系图线.若物块与木板间的动摩擦因数为0.2,假定物块与木板间的最大静摩擦力始终等于滑动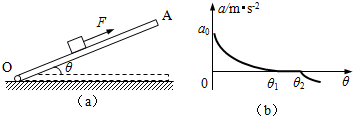 摩擦力,g取10m/s2.试问:
摩擦力,g取10m/s2.试问:
(1)图(b)中图线与纵坐标交点a0多大?
(2)图(b)中图线与θ轴交点坐标分别为θ1和θ2,木板处于该两个角度时的摩擦力指向何方?说明在斜面倾角处于θ1和θ2之间时物块的运动状态.
(3)若木板长LOA=2m,水平放置,物块在F的作用下由O点开始运动,为保证物块不冲出木板A端,力F最多作用多长时间?
 摩擦力,g取10m/s2.试问:
摩擦力,g取10m/s2.试问:(1)图(b)中图线与纵坐标交点a0多大?
(2)图(b)中图线与θ轴交点坐标分别为θ1和θ2,木板处于该两个角度时的摩擦力指向何方?说明在斜面倾角处于θ1和θ2之间时物块的运动状态.
(3)若木板长LOA=2m,水平放置,物块在F的作用下由O点开始运动,为保证物块不冲出木板A端,力F最多作用多长时间?
分析:(1)图线与纵坐标交点处的横坐标为0,即木板水平放置,此时对应的加速度为a0,分析此时物块的受力根据牛顿第二定律求出对应的加速度即可;
(2)当摩擦力沿斜面向下且加速度为零时木板倾角为θ1,当摩擦力沿斜面向上且加速度为零时木板倾角为θ2,这时物块处于静止状态;
(3)根据牛顿第二定律分别求出有F和撤去F时的加速度,根据匀变速直线运动的基本公式求出这两个过程的位移,根据两段位移之和为L求解.
(2)当摩擦力沿斜面向下且加速度为零时木板倾角为θ1,当摩擦力沿斜面向上且加速度为零时木板倾角为θ2,这时物块处于静止状态;
(3)根据牛顿第二定律分别求出有F和撤去F时的加速度,根据匀变速直线运动的基本公式求出这两个过程的位移,根据两段位移之和为L求解.
解答:解:(1)θ=00时,木板水平放置,物块在水平方向受到拉力F和滑动摩擦力f作用,已知F=8N,滑动摩擦力f=μN=μmg,所以根据牛顿第二定律物块产生的加速度:a0=
=
=6m/s2
(2)当斜面倾角为θ1时,摩擦力沿斜面向下;当斜面倾角为θ2时,摩擦力沿斜面向上;当斜面倾角在θ1和θ2之间时,物块处于静止状态.
(3)设F作用的时间为t0,位移为s0.撤去F作用后物块加速度为a,运动时间为t,位移为s
s0=
a0t02
v0=a0t0
撤去外力F后,物块在滑动摩擦力作用下做减速运动,由于滑动摩擦力f=μmg,所以此时物体产生的加速度大小:
a=μg=0.2×10=2m/s2
物块做匀减速运动产生的位移s=a0t0t-
at2
物体由静止开始加速,撤去外力F后在摩擦力作用下减速至停止,故速度关系满足:
v0=a0t0=at
t=
代入:s0+s=LOA
有:
a0t02+a0t0t-
at2=LOA
×6×T02+6×t0×
-
×2×(
)2=2
解得:t0=
≈0.41s
答:(1)图(b)中图线与纵坐标交点a0=6m/s2
(2)图(b)中图线与θ轴交点坐标分别为θ1和θ2,木板在θ1时所受摩擦力沿木板向下,在θ2时沿木板向上,斜面倾角处于θ1和θ2之间时物块处于静止状态;
(3)若木板长LOA=2m,水平放置,物块在F的作用下由O点开始运动,为保证物块不冲出木板A端,力F最多作用0.41s.
| F-μmg |
| m |
| 8-0.2×1×10 |
| 1 |
(2)当斜面倾角为θ1时,摩擦力沿斜面向下;当斜面倾角为θ2时,摩擦力沿斜面向上;当斜面倾角在θ1和θ2之间时,物块处于静止状态.
(3)设F作用的时间为t0,位移为s0.撤去F作用后物块加速度为a,运动时间为t,位移为s
s0=
| 1 |
| 2 |
v0=a0t0
撤去外力F后,物块在滑动摩擦力作用下做减速运动,由于滑动摩擦力f=μmg,所以此时物体产生的加速度大小:
a=μg=0.2×10=2m/s2
物块做匀减速运动产生的位移s=a0t0t-
| 1 |
| 2 |
物体由静止开始加速,撤去外力F后在摩擦力作用下减速至停止,故速度关系满足:
v0=a0t0=at
t=
| a0t0 |
| a |
代入:s0+s=LOA
有:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 6t0 |
| 2 |
| 1 |
| 2 |
| 6t0 |
| 2 |
解得:t0=
| ||
| 6 |
答:(1)图(b)中图线与纵坐标交点a0=6m/s2
(2)图(b)中图线与θ轴交点坐标分别为θ1和θ2,木板在θ1时所受摩擦力沿木板向下,在θ2时沿木板向上,斜面倾角处于θ1和θ2之间时物块处于静止状态;
(3)若木板长LOA=2m,水平放置,物块在F的作用下由O点开始运动,为保证物块不冲出木板A端,力F最多作用0.41s.
点评:本题主要考查了牛顿第二定律及运动学基本公式的直接应用,要求同学们能根据图象得出有效信息,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
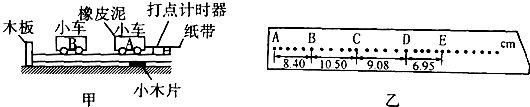
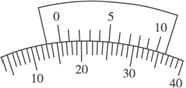
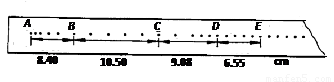
 小明同学用如图所示的实验装置验证规律:物体质量一定,其加速度与所受合力成正比.
小明同学用如图所示的实验装置验证规律:物体质量一定,其加速度与所受合力成正比.