题目内容
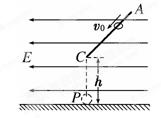
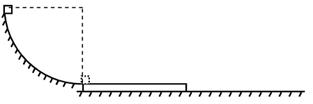
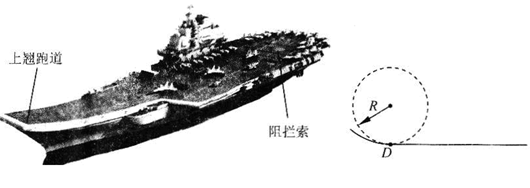
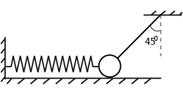
如图所示，倾角为45°的粗糙斜面AB底端与半径R=0.4m的光滑半圆轨道BC平滑相接，O为轨道圆心，BC为圆轨道直径且处于竖直平面内，A、C两点等高．质量m=1kg的滑块从A点由静止开始下滑，恰能滑到与O等高的D点，g取10m/s2．求：
（1）求滑块与斜面间的动摩擦因数μ；
（2）若使滑块能到达C点，求滑块至少从离地多高处由静止开始下滑；
（3）若滑块离开C处后恰能垂直打在斜面上，求滑块经过C点时对轨道的压力．
（1）0.5 （2）2m（3）3.3N
解析试题分析：（1）由A到D，根据动能定理可得
解得
（2）若滑块恰能到达C点，根据牛顿定律 
,解得
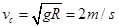
从高为H的最高点到C的过程，根据动能定理 
，解得H=2m
(3)l离开C点后滑块做平抛运动，垂直打到斜面上时有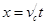 
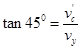
解得 
在C点，根据牛顿第二定律有
求得：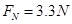
由牛顿第三定律可知，滑块对轨道的压力为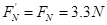
方向竖直向上
考点：此题考查圆周运动及平抛运动；考查牛顿定律、动能定理等物理规律。
练习册系列答案
阅读快车系列答案
相关题目
，且每隔T/2变向1次。现将质量为m的带正电，且电荷量为q的粒子束从AB的中点O以平行于金属板的方向OO′射入，设粒子能全部打在靶上而且所有粒子在A、B间的飞行时间均为T。不计重力的影响，试问：
；
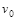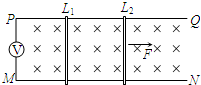
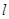的正方形方框，方框内有大小可调、方向竖直向下的匀强磁场，方框左边界的中点有一小孔，恰能让质量为m、带电量为+q的小球b（可视为质点）无阻碍的通过。初始时，小球b静止在小孔处。边界线MN的左侧有一范围足够大的匀强电场区域，电场的电场强度为E，方向水平向左，MN的右侧与方框的左侧间的距离可忽略不计。现有另一质量为
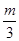、不带电的小球a以速度
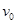正对b球运动。设所有的碰撞均无能量损失和电量的转移，不计一切摩擦，则：
、
；
；
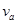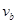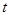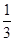.(取sin53°＝0.8，g＝10m/s2)求：
