题目内容
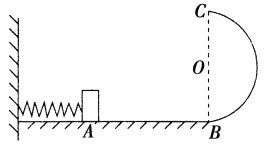
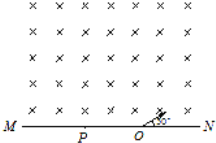
【题目】如图甲所示,倾斜传送带倾角θ=37°,两端A、B间距离L=4 m,传送带以4 m/s的速度顺时针转动,质量为1 kg的滑块从传送带顶端B点由静止释放后下滑,到A端时用时2 s,g取10 m/s2,sin 37°=0.6,cos 37°=0.8.

(1)求滑块与传送带间的动摩擦因数;
(2)若该滑块在传送带的底端 A点,如图乙所示,现用一沿传送带向上的大小为6 N的恒定拉力F拉滑块,使其由静止开始沿传送带向上运动,当滑块速度与传送带速度相等时,撤去拉力,则当滑块到传送带顶端时,滑块速度为多大?
【答案】(1)0.5(2)![]()
【解析】
(1)滑块从B点下滑的过程中,有
mgsin θ-μmgcos θ=ma1
L=![]() a1t12
a1t12
解得a1=2 m/s2,μ=0.5
(2)当用拉力F拉滑块时,有
F+μmgcos θ-mgsin θ=ma2
解得a2=4 m/s2
当滑块速度与传送带速度相等时,滑块运动的位移
x1=![]() =2 m
=2 m
撤去拉力后,滑块开始向上做匀减速运动,加速度大小等于a1,向上运动的位移大小为
x2=L-x1=2 m
由v2-vB2=2a1x2
解得vB=2![]() m/s
m/s

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目