题目内容
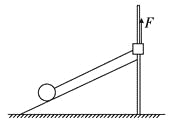
【题目】如图所示,粗糙水平面上放置一个质量M=2 kg、长度L= 5 m的木板A,可视为质点的物块B放在木板A的最左端,其质量m=1 kg。已知A、B间动摩擦因数为μ1=0.2,A与水平地面间的动摩擦因数为μ2=0.4。开始时A、B均处于静止状态,当B获得水平向右的初速度v0=8 m/s的同时,对A施加水平向右的恒力F,取g=10 m/s2,求:

(1)为使物块B不从木板A的右端滑出,力F的最小值为多大?
(2)若F=22 N,则物块B的最大速度为多大?
【答案】(1)18.8N(2)10m/s
【解析】(1)物块B在木板A上做匀减速直线运动,由牛顿第二定律可知:
μ1mg=ma1
解得:a1=2m/s2
物块B滑到A的右端时A、B速度相等,则物块B刚好不从木板A的右端滑出,A、B相对位移为木板长L,木板A的加速度为a2 ,由速度公式和位移公式可知:
木板A的速度为:v= a2t
物块B的速度为:v=v0-a1t
木板A的位移为: ![]()
物块B的位移为: ![]()
A、B的相对位移为木板长L: L=xB-xA
联立以上各式解得: ![]()
对木板A,由牛顿第二定律可知:F+μ1mg-μ2(m+M)g=Ma2
解得:F=18.8N
(2)物块B在木板A上先做匀减速直线运动,加速度为a1=2m/s2;木板A做匀加速直线运动。对木板A,由牛顿第二定律可得:
F+μ1mg-μ2(m+M)g=Ma3
解得:a3=6m/s2
设经过时间t1,A、B两物体速度相同,大小都为v1
v1=v0-a1t1
v1= a3t1
联立解得:t1=1s
v1=6m/s
在此过程中A、B的位移分别为xA1、xB1,则:
![]()
![]()
A、B间的相对位移为:Δx1=xB1-xA1
A、B速度相同后,木板A以a4的加速度继续匀加速运动,由牛顿运动定律可知:
F-μ1mg-μ2(m+M)g=Ma4
解得:a4=4m/s 2
由于a4>a1,所以物块B也向右做匀加速运动,但相对木板A向左运动,经时间t2后物块B会从木板A的左端滑出,在这段时间内:
木板A的位移为: ![]()
物块B的位移为: ![]()
A、B间的相对位移Δx2=Δx1,则:Δx1=xA2-xB2
联立解得:t2=2s
物块B从木板A的左端滑出时的速度为:
v3=v1+a1t2
解得:v3=10m/s
物块B从木板A的左端滑出后落到地面上做匀减速运动,所以整个过程中,物块B从木板A的左端滑出时的速度为最大速度:10m/s