题目内容
 (2003?广州一模)半径为R的玻璃半圆柱体,横截面如图所示,圆心为O,两条平行单色红光沿截面射向圆柱面,方向与底面垂直,光线1的入射点A为圆柱面的顶点,光线2的入射点为B,∠AOB=60°,已知该玻璃对红光的折射率n=
(2003?广州一模)半径为R的玻璃半圆柱体,横截面如图所示,圆心为O,两条平行单色红光沿截面射向圆柱面,方向与底面垂直,光线1的入射点A为圆柱面的顶点,光线2的入射点为B,∠AOB=60°,已知该玻璃对红光的折射率n=| 3 |
(1)求两条光线经柱面和底面折射后的交点与O点的距离d;
(2)若入射的是单色蓝光,则距离d将比上面求得的结果大还是小?
分析:(1)光线1通过玻璃砖后不偏折.光线2在圆柱面上的入射角为60°,根据折射定律求出折射角,由几何知识求出在底面上的入射角,再由折射定律求出折射角,作出光路图.根据几何关系求解d.
(2)若入射的单色蓝光,光线1仍不偏折,由于介质对蓝光的折射率大于介质对红光的折射率,光线2偏折得更厉害,d更小.
(2)若入射的单色蓝光,光线1仍不偏折,由于介质对蓝光的折射率大于介质对红光的折射率,光线2偏折得更厉害,d更小.
解答:解:(1)光线1通过玻璃砖后不偏折.光线2在圆柱面上的入射角θ1=60°,由折射定律得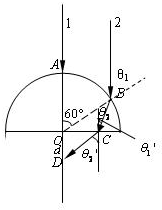
n=
,得到sinθ2=
=
得θ2=30°
由几何知识得 θ1′=60°-θ2=30°
又由折射定律得
n=
代入解得θ2′=60°
由于△BOC是等腰三角形,则
=
=
R
所以d=
cotθ2′=
R.
(2)若入射的单色蓝光,光线1仍不偏折,由于介质对蓝光的折射率大于介质对红光的折射率,光线2偏折得更厉害,θ2′更大,d更小.
答:(1)两条光线经柱面和底面折射后的交点与O点的距离d=
R;
(2)若入射的是单色蓝光,则距离d将比上面求得的结果小.

n=
| sinθ1 |
| sinθ2 |
| sinθ1 |
| n |
| 1 |
| 2 |
得θ2=30°
由几何知识得 θ1′=60°-θ2=30°
又由折射定律得
n=
| sinθ2′ |
| sinθ1′ |
由于△BOC是等腰三角形,则
. |
| OC |
| ||
| cos30° |
| ||
| 3 |
所以d=
. |
| OC |
| 1 |
| 3 |
(2)若入射的单色蓝光,光线1仍不偏折,由于介质对蓝光的折射率大于介质对红光的折射率,光线2偏折得更厉害,θ2′更大,d更小.
答:(1)两条光线经柱面和底面折射后的交点与O点的距离d=
| 1 |
| 3 |
(2)若入射的是单色蓝光,则距离d将比上面求得的结果小.
点评:本题其实是光的色散问题,关键是作出光路图,运用几何知识辅助分析.中等难度.

练习册系列答案
相关题目
 (2003?广州一模)如图所示,质量相同的木块A、B用轻弹簧连接置于光滑的水平面上,开始弹簧处于自然状态,现用水平恒力F推木块A,则从开始到弹簧第一次被压缩到最短的过程中,以下说法正确的是( )
(2003?广州一模)如图所示,质量相同的木块A、B用轻弹簧连接置于光滑的水平面上,开始弹簧处于自然状态,现用水平恒力F推木块A,则从开始到弹簧第一次被压缩到最短的过程中,以下说法正确的是( ) (2003?广州一模)有一种玩具结构如图所示,竖直放置的光滑铁圆环的半径为R=20cm,环上穿有一个带孔的小球m,仅能沿环做无摩擦滑动.如果圆环绕着通过环心的竖直轴O1O2以10rad/s的角速度旋转(g=10m/s2),则小球相对环静止时和环心O的连线与O1O2的夹角θ是( )
(2003?广州一模)有一种玩具结构如图所示,竖直放置的光滑铁圆环的半径为R=20cm,环上穿有一个带孔的小球m,仅能沿环做无摩擦滑动.如果圆环绕着通过环心的竖直轴O1O2以10rad/s的角速度旋转(g=10m/s2),则小球相对环静止时和环心O的连线与O1O2的夹角θ是( ) (2003?广州一模)如图所示,在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场,第三象限有沿Y轴负方向的匀强电场,第四象限内无电场和磁场.质量为m、带电量为q的粒子从M点以速度v0沿x轴负方向进入电场,不计粒子的重力,粒子经N、P最后又回到M点.设OM=L,ON=2L,则:
(2003?广州一模)如图所示,在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场,第三象限有沿Y轴负方向的匀强电场,第四象限内无电场和磁场.质量为m、带电量为q的粒子从M点以速度v0沿x轴负方向进入电场,不计粒子的重力,粒子经N、P最后又回到M点.设OM=L,ON=2L,则: