题目内容
10.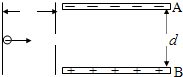 有一电子从静止开始经电压U1加速后,进入两块间距为d,电压为U2的平行金属板间,若电子从两板正中间垂直电场方向射入,且正好能穿出电场,设电子的电量大小为e质量为m.求:
有一电子从静止开始经电压U1加速后,进入两块间距为d,电压为U2的平行金属板间,若电子从两板正中间垂直电场方向射入,且正好能穿出电场,设电子的电量大小为e质量为m.求:(1)电子经电压U1加速后的速度v;
(2)电子在第二个电场中的运动时间;
(3)电子穿出右边电场时的动能.
分析 (1)电子在加速电场中加速,由动能定理可以求出速度.
(2)电子在偏转电场中做类平抛运动,由类平抛运动规律可以求出运动时间.
(3)由动能定理可以求出电子离开电场时的动能.
解答 解:(1)电子的质量为m,由动能定理得:
$e{U_1}=\frac{1}{2}mv_{\;}^2$,
解得:v=$\sqrt{\frac{{2e{U_1}}}{m}}$;
(2)因为电子正好能穿出电场,则电子竖直偏移量为$\frac{d}{2}$,
由类平抛运动得:$\frac{d}{2}=\frac{1}{2}a{t^2}=\frac{1}{2}\frac{{e{U_2}}}{dm}{t^2}$,
解得:t=d$\sqrt{\frac{m}{{e{u_2}}}}$;
(3)由动能定理得:${E_K}={W_1}+{W_2}=e{U_1}+e\frac{U_2}{d}×\frac{d}{2}=e\frac{{2{U_1}+{U_2}}}{2}$;
答:(1)电子经电压U1加速后的速度v为$\sqrt{\frac{{2e{U_1}}}{m}}$;
(2)电子在第二个电场中的运动时间为d$\sqrt{\frac{m}{{e{u_2}}}}$;
(3)电子穿出右边电场时的动能为:e(U1+$\frac{1}{2}$U2).
点评 本题考查了电子在电场中的运动,电子在加速电场中加速、在偏转电场中做类平抛运动,分析清楚电子的运动过程是正确解题的关键,应用动能定理与类平抛运动规律可以解题.

练习册系列答案
相关题目
20.关于牛顿第三定律,下列说法正确是( )
| A. | 作用力大时,反作用力小 | |
| B. | 作用力和反作用力是作用在同一个物体上的 | |
| C. | 作用力和反作用力的方向总是相反的 | |
| D. | 作用力与反作用力大小相等,作用在同一条直线上 |
18.一个面积为S的闭合线圈放在磁感应强度为B的匀强磁场中,已知线圈平面与磁感线的夹角为α,则穿过此线圈的磁通量为( )
| A. | BS | B. | BScosα | C. | BSsinα | D. | 0 |
5. 一个验电器带电后两个金箔张开一定的角度,如图所示,将用丝绸摩擦过的玻璃棒从远处向验电器的小球移近(但不与小球接触)的过程中,观察到验电器的金箔张角先减小到0,然后再张开,张角变大,则( )
一个验电器带电后两个金箔张开一定的角度,如图所示,将用丝绸摩擦过的玻璃棒从远处向验电器的小球移近(但不与小球接触)的过程中,观察到验电器的金箔张角先减小到0,然后再张开,张角变大,则( )
 一个验电器带电后两个金箔张开一定的角度,如图所示,将用丝绸摩擦过的玻璃棒从远处向验电器的小球移近(但不与小球接触)的过程中,观察到验电器的金箔张角先减小到0,然后再张开,张角变大,则( )
一个验电器带电后两个金箔张开一定的角度,如图所示,将用丝绸摩擦过的玻璃棒从远处向验电器的小球移近(但不与小球接触)的过程中,观察到验电器的金箔张角先减小到0,然后再张开,张角变大,则( )| A. | 验电器原来带正电荷 | |
| B. | 验电器金箔一直带负电荷 | |
| C. | 验电器的金箔原来带正电荷,后来带负电荷 | |
| D. | 验电器的金箔原来带负电荷,后来带正电荷 |
2.关于汽车的功率P、速度v和牵引力F三者之间的关系,下列说法中正确的是( )
| A. | 当汽车的牵引力一定时,若汽车做加速运动,功率P不断增大 | |
| B. | 当汽车的功率一定时,汽车的牵引力越大,速度越小 | |
| C. | 当汽车匀速运动时,汽车所受阻力越小,汽车的功率越大 | |
| D. | 当汽车所受阻力一定时,汽车速度越大,其功率也越大 |
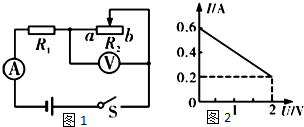 张欢在做“伏安法测电阻”实验时,按如图1所示接了电路,其中R1为定值待测电阻,R2为滑动变阻器,电源电压不变.闭合开关S后,滑片P从a端移动到b端,电流表示数I与电压表示数U的变化关系如图2所示,则电源电压为3V,R2的最大阻值为10Ω,R1的阻值为5Ω.
张欢在做“伏安法测电阻”实验时,按如图1所示接了电路,其中R1为定值待测电阻,R2为滑动变阻器,电源电压不变.闭合开关S后,滑片P从a端移动到b端,电流表示数I与电压表示数U的变化关系如图2所示,则电源电压为3V,R2的最大阻值为10Ω,R1的阻值为5Ω. 如图所示是等离子体发电机的示意图,磁感应强度为B,两极板间距离为d,要使输出电压为U,则等离子体的速度v为$\frac{U}{dB}$,a是电源的正极.
如图所示是等离子体发电机的示意图,磁感应强度为B,两极板间距离为d,要使输出电压为U,则等离子体的速度v为$\frac{U}{dB}$,a是电源的正极.