题目内容
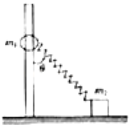
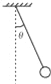
【题目】悬挂在O点的一根不可伸长的绝缘细线下端有一个质量为m、带电量为﹣q的小球，若在空间加一匀强电场，则小球静止时细线与竖直方向夹角为θ，如图所示，求：
（1）所加匀强电场场强最小值的大小和方向；
（2）若在某时刻突然撤去电场，当小球运动到最低点时，小球对细线的拉力为多大．
【答案】（1）所加匀强电场场强最小值的大小为
，方向垂直细线向下；（2）mg（3﹣2cosθ）
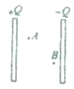
【解析】（1）对小球实力分析，受重力、电场力和拉力，如图所示：
从图中可以看出，当电场力方向与细线垂直时，电场力最小，电场强度最小，根据共点力平衡条件，有：
mgsinθ=qE
解得：E=
（2）某时刻突然撤去电场，小球小角度摆动，只有重力做功，机械能守恒，根据守恒定律，有：
mgL（1﹣cosθ）=
在最低点，小球受重力和拉力，合力提供向心力，根据牛顿第二定律，有：
T﹣mg= 
联立解得：T=mg（3﹣2cosθ）
根据牛顿第三定律，小球对细线的拉力为mg（3﹣2cosθ）
练习册系列答案
相关题目
