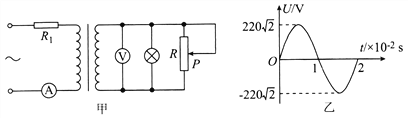
题目内容
【题目】如图所示,内壁光滑的圆锥筒,圆锥的轴线竖直,顶角为2θ=60°,底面半径为R,在底面圆心O处,系一个轻质细线,长也为R,细线的另一端连一个小球,小球可视为质点。现给小球一个初速度,使其做水平圆周运动,已知重力加速度为g,则:
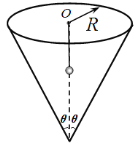
(1)要使小球不碰到锥筒,小球的线速度不超过多大?
(2)要使细线无拉力,小球的线速度应满足什么条件?
【答案】(1)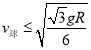 (2)
(2)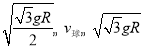
【解析】
(1)小球恰好与筒壁接触,但与筒壁无作用力,设此时小球的速度为![]() ,受力如图1,
,受力如图1,
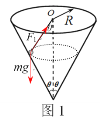
由牛顿定律得![]()
解得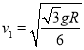
所以,小球速度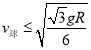 ,小球不会碰到筒壁
,小球不会碰到筒壁
(2)小球恰好与筒壁接触,但线的拉力为零,设此时小球的速度为![]() ,受力如图2,
,受力如图2,
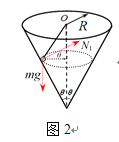
由牛顿定律得![]()
解得: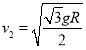
当细线达到水平时,线的拉力为零。设此时小球的速度为![]() ,受力如图3
,受力如图3
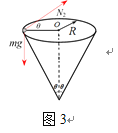
由牛顿定律得![]()
解得![]()
所以要使细线无拉力,小球的速度应满足: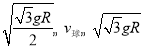

练习册系列答案
相关题目