题目内容
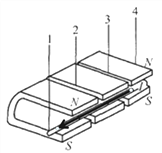
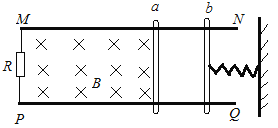
【题目】某同学利用电磁感应知识设计了一个测速仪。其简化模型如图所示,间距为L的两根水平固定放置的平行光滑的金属导轨MN、PQ,导轨的右端连接一个定值电阻,阻值为R,导体棒a垂直导轨放置在导轨上,在a棒左侧和导轨间存在竖直向下的匀强磁场,磁感应强度为B,在a棒右侧有一绝缘棒b,b棒与固定在墙上的轻弹簧相连但不粘连,弹簧处于压缩状态且被锁定。现解除锁定,b棒在弹簧的作用下向左移动,脱离弹簧后以速度v0与a棒发生碰撞粘在一起。已知a、b棒的质量分别为m、M,碰撞前后,棒始终垂直导轨,a棒在导轨间的电阻为r,导轨电阻和空气阻力均忽略不计。求:
(1)弹簧的弹性势能和a棒中电流的方向;
(2)从a棒开始运动到停止过程中,a棒产生的焦耳热Q;
(3)若a棒向左滑行的距离为x,通过定值电阻的电量q;
(4)在满足(3)的条件下,a棒向左滑行距离x与b棒的速度v0的函数关系式。
【答案】(1)从上端流向下端(2)![]() (3)
(3)![]() (4)
(4)![]()
【解析】(1)对b棒由能量守恒定律,得弹簧的弹性势能![]()
由右手定则知,a棒中电流的方向:从上端流向下端
(2)b棒与a棒相碰撞时,由动量守恒定律知![]()
又电路产生的总热量为![]()
a棒产生的焦耳热![]()
联立得![]()
(3)若a棒向左滑行的距离为x,则通过定值电阻的电量
![]()
![]()
得![]()
(4)对a棒向左滑动的过程中,由牛顿第二定律知
![]()
又![]() ,
,![]()
联立得![]()
两边求和得![]()
得![]()
代入![]() ,得
,得![]()

练习册系列答案
相关题目