题目内容
13.如图所示,直线MN表示一条平直公路,甲、乙两辆汽车原来停在A、B两处,A、B间的距离为85m,现甲车先开始向右做匀加速直线运动,加速度a1=2.5m/s2,甲车运动6s时,乙车立即开始向右做匀加速直线运动,加速度a2=5m/s2,求两辆汽车相遇处距A处的距离.
分析 先求出甲车运动6.0s时的位移,看此时有没有相遇,如没有设此后用时间t与乙车相遇,根据时间和位移的关系列方程即可解题.
解答 解:甲车运动6s的位移为:${s_0}=\frac{1}{2}{a_1}{t_0}^2=45m$
尚未追上乙车,设此后用时间t与乙车相遇,则有:$\frac{1}{2}{a_1}{(t+{t_0})^2}=\frac{1}{2}{a_2}{t^2}+85m$
将上式代入数据并展开整理得:t2-12t+32=0
解得:t1=4s,t2=8s
t1、t2、都有意义,t1=4s时,甲车追上乙车;t2=8s时,乙车追上甲车再次相遇.
第一次相遇地点距A的距离为:${s_1}=\frac{1}{2}{a_1}{({t_1}+{t_0})^2}$=125m
第二次相遇地点距A的距离为:${s_2}=\frac{1}{2}{a_1}{({t_2}+{t_0})^2}$=245m.
答:两辆汽车相遇处距A处的距离分别为125m或245m.
点评 本题是追击问题,要注意最后求出的两个时间都有意义,表明两车可以相遇两次,第一次时甲追上乙,第二次时乙追上甲.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
4.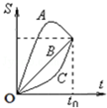 A、B、C三个物体从同一点出发,沿着一条直线运动的位移-时间(S-t)图象如图所示,下列说法中正确的是( )
A、B、C三个物体从同一点出发,沿着一条直线运动的位移-时间(S-t)图象如图所示,下列说法中正确的是( )
 A、B、C三个物体从同一点出发,沿着一条直线运动的位移-时间(S-t)图象如图所示,下列说法中正确的是( )
A、B、C三个物体从同一点出发,沿着一条直线运动的位移-时间(S-t)图象如图所示,下列说法中正确的是( )| A. | 三者者的位移不相等 | |
| B. | A物体做曲线运动 | |
| C. | 三个物体在0~t0时间内的平均速度vA>vC>vB | |
| D. | 三个物体在0~t0时间内的平均速度vA=vB=vC |
1.如图所示为在同一直线上运动的A、B两质点的x-t图象.由图可知( )
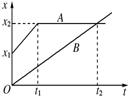

| A. | B在t2时刻追上A,并在此后跑在A的前面 | |
| B. | t=0时,A在B的后面 | |
| C. | B开始运动的速度比A小,t2时刻后才大于A的速度 | |
| D. | A运动的速度始终比B大 |
 一长为L的细线,上端固定,下端拴一质量为m、带电荷量为q的小球,处于如图所示的水平向右的匀强电场中.开始时,将细线与小球拉成水平,小球静止在A点,释放后小球由静止开始向下摆动,当细线转过60°角时,小球到达B点速度恰好为零.试求:
一长为L的细线,上端固定,下端拴一质量为m、带电荷量为q的小球,处于如图所示的水平向右的匀强电场中.开始时,将细线与小球拉成水平,小球静止在A点,释放后小球由静止开始向下摆动,当细线转过60°角时,小球到达B点速度恰好为零.试求: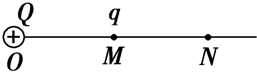 在真空中O点放一个电荷Q=+1.0×10-9C,直线MN通过O点,OM的距离r=30cm,M点放一个点电荷q=-1.0×10-10C,如图所示.
在真空中O点放一个电荷Q=+1.0×10-9C,直线MN通过O点,OM的距离r=30cm,M点放一个点电荷q=-1.0×10-10C,如图所示.