题目内容
 如图有一半径为r=0.2m的圆柱体绕竖直轴OO′以ω=9rad/s的欠速度匀速转动,今用力F将质量为1kg的物体A压圆柱侧面,使其以v0=2.4m/s的速度匀速下降,若物体A与圆柱面的摩擦因数μ=0.25,求力F的大小.(已知物体A在水平方向受光滑挡板的作用,不能随轴一起转动).
如图有一半径为r=0.2m的圆柱体绕竖直轴OO′以ω=9rad/s的欠速度匀速转动,今用力F将质量为1kg的物体A压圆柱侧面,使其以v0=2.4m/s的速度匀速下降,若物体A与圆柱面的摩擦因数μ=0.25,求力F的大小.(已知物体A在水平方向受光滑挡板的作用,不能随轴一起转动).
解:在水平方向圆柱体有垂直纸面向里的速度,A相对圆柱体有垂直纸面向外的速度为v′,
则v′=ωr=9rad/s×0.2m=1.8m/s;
在竖直方向有向下的速度 v0=2.4m/s
合速度的大小为v=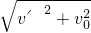 =3m/s
=3m/s
设合速度与竖直方向的夹角为θ,则有;cosθ= =
=
所以A所受的滑动摩擦力方向与竖直方向的夹角也为θ.
A做匀速运动,竖直方向平衡,则有
Ffcosθ=mg,
得 Ff= =12.5N
=12.5N
另Ff=μFN,FN=F,
所以有:F= =50N
=50N
答:力F的大小为50N.
分析:物体A匀速下降,受力平衡,物体受到重力、外力F、圆柱体的支持力和滑动摩擦力,而滑动摩擦力方向与物体相对于圆柱体的速度方向相反.物体A既以v0=2.4m/s的速度竖直下降,又相对圆柱体转动,先由 v′=ωr求出A相对圆柱体垂直纸面向外的速度v′,得到合速度v,由cosθ= =
= ,求出合速度与竖直方向的夹角θ,即可确定出滑动摩擦力的方向,再根据平衡条件和摩擦力公式Ff=μFN,求解F的大小.
,求出合速度与竖直方向的夹角θ,即可确定出滑动摩擦力的方向,再根据平衡条件和摩擦力公式Ff=μFN,求解F的大小.
点评:本题关键是运用运动的合成法确定合速度的方向,得到滑动摩擦力的方向,要有空间想象能力.
则v′=ωr=9rad/s×0.2m=1.8m/s;
在竖直方向有向下的速度 v0=2.4m/s
合速度的大小为v=
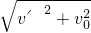 =3m/s
=3m/s设合速度与竖直方向的夹角为θ,则有;cosθ=
 =
=
所以A所受的滑动摩擦力方向与竖直方向的夹角也为θ.
A做匀速运动,竖直方向平衡,则有
Ffcosθ=mg,
得 Ff=
 =12.5N
=12.5N另Ff=μFN,FN=F,
所以有:F=
 =50N
=50N答:力F的大小为50N.
分析:物体A匀速下降,受力平衡,物体受到重力、外力F、圆柱体的支持力和滑动摩擦力,而滑动摩擦力方向与物体相对于圆柱体的速度方向相反.物体A既以v0=2.4m/s的速度竖直下降,又相对圆柱体转动,先由 v′=ωr求出A相对圆柱体垂直纸面向外的速度v′,得到合速度v,由cosθ=
 =
= ,求出合速度与竖直方向的夹角θ,即可确定出滑动摩擦力的方向,再根据平衡条件和摩擦力公式Ff=μFN,求解F的大小.
,求出合速度与竖直方向的夹角θ,即可确定出滑动摩擦力的方向,再根据平衡条件和摩擦力公式Ff=μFN,求解F的大小.点评:本题关键是运用运动的合成法确定合速度的方向,得到滑动摩擦力的方向,要有空间想象能力.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 如图有一半径为r=0.2m的圆柱体绕竖直轴OO′以ω=9rad/s的欠速度匀速转动,今用力F将质量为1kg的物体A压圆柱侧面,使其以v0=2.4m/s的速度匀速下降,若物体A与圆柱面的摩擦因数μ=0.25,求力F的大小.(已知物体A在水平方向受光滑挡板的作用,不能随轴一起转动).
如图有一半径为r=0.2m的圆柱体绕竖直轴OO′以ω=9rad/s的欠速度匀速转动,今用力F将质量为1kg的物体A压圆柱侧面,使其以v0=2.4m/s的速度匀速下降,若物体A与圆柱面的摩擦因数μ=0.25,求力F的大小.(已知物体A在水平方向受光滑挡板的作用,不能随轴一起转动).


