题目内容
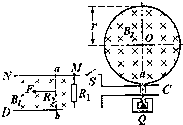 如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距离L=0.2m,电阻R1=0.4Ω,导轨上静止放置一质量m=0.1kg,电阻R2=0.1Ω的金属杆ab,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆ab,使之由静止开始运动,最终以8m/s的速度做匀速直线运动.若此时闭合开关S,释放的α粒子经加速电场C加速从a孔对着圆心O进入半径r=
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距离L=0.2m,电阻R1=0.4Ω,导轨上静止放置一质量m=0.1kg,电阻R2=0.1Ω的金属杆ab,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆ab,使之由静止开始运动,最终以8m/s的速度做匀速直线运动.若此时闭合开关S,释放的α粒子经加速电场C加速从a孔对着圆心O进入半径r=| 3 |
(1)ab杆做匀速直线运动过程中,外力F的功率;
(2)α射线源Q是钍核
294 63 |
295 56 |
256 60 |
258 58 |
(3)若α粒子与圆筒壁碰撞5次后恰又从a孔背离圆心射出,忽略α粒子进入加速电场的初速度,求磁感应强度B2.
分析:(1)ab杆做匀速直线运动过程中,外力F与安培力二力平衡,推导出安培力表达式,即可求得外力的大小,由P=Fv求出功率.
(2)根据质量数守恒和电荷数配平,确定α粒子符号.
(3)根据欧姆定律求出加速电场的电压,由动能定理求出α粒子进入磁场的速度.若α粒子与圆筒壁碰撞5次后恰又从a孔背离圆心射出,则粒子与圆筒的碰撞点和a点将圆筒6等分,根据几何关系求出轨迹半径,由牛顿第二定律求磁感应强度B2.
(2)根据质量数守恒和电荷数配平,确定α粒子符号.
(3)根据欧姆定律求出加速电场的电压,由动能定理求出α粒子进入磁场的速度.若α粒子与圆筒壁碰撞5次后恰又从a孔背离圆心射出,则粒子与圆筒的碰撞点和a点将圆筒6等分,根据几何关系求出轨迹半径,由牛顿第二定律求磁感应强度B2.
解答: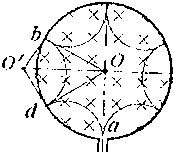 解:(1)当ab杆匀速运动时,外力F与安培力二力平衡,则有 F杆=FB ①
解:(1)当ab杆匀速运动时,外力F与安培力二力平衡,则有 F杆=FB ①
FB=B1IL ②
I=
③
E=B1Lv ④
联立得:F杆=FB=
外力F的功率P=F外v ⑤
则得 P=
将已知条件代入上式解得 P=1.28W
(2)根据质量数守恒和电荷数配平得:α粒子符号是
He.
(3)此时回路电流强度为 I=
=
=
A=1.6A
加速电场的电压为 U=IR1=1.6×0.4V=0.64V
根据动能定理:q0U=
mav2
α粒子从a孔进入磁场的速度 v=
=
=8.0×103m/s
由题意知:α粒子与圆筒壁碰撞5次后从a孔离开磁场,画出轨迹,由几何关系求得∠dOb=60°
轨迹半径 R′=
r=1m
又qαvB=mα
故 B2=
=
=1.6×10-4T
答:
(1)ab杆做匀速直线运动过程中,外力F的功率为1.28W;
(2)α射线源Q是钍核
Th发生衰变生成镭核
Ha并粒出一个α粒子,完成下列钍核的衰变方程
Th→
Ra+
He;
(3)磁感应强度B2为1.6×10-4T.
 解:(1)当ab杆匀速运动时,外力F与安培力二力平衡,则有 F杆=FB ①
解:(1)当ab杆匀速运动时,外力F与安培力二力平衡,则有 F杆=FB ①FB=B1IL ②
I=
| E |
| R1+R2 |
E=B1Lv ④
联立得:F杆=FB=
| ||
| R1+R2 |
外力F的功率P=F外v ⑤
则得 P=
| ||
| R1+R2 |
将已知条件代入上式解得 P=1.28W
(2)根据质量数守恒和电荷数配平得:α粒子符号是
4 2 |
(3)此时回路电流强度为 I=
| E |
| R1+R2 |
| B1Lv |
| R1+R2 |
| 0.5×0.2×8 |
| 0.4+0.1 |
加速电场的电压为 U=IR1=1.6×0.4V=0.64V
根据动能定理:q0U=
| 1 |
| 2 |
α粒子从a孔进入磁场的速度 v=
|
|
由题意知:α粒子与圆筒壁碰撞5次后从a孔离开磁场,画出轨迹,由几何关系求得∠dOb=60°
轨迹半径 R′=
| ||
| 3 |
又qαvB=mα
| v2 |
| R′ |
故 B2=
| mav |
| q0R′ |
| 6.4×10-27×8.0×103 |
| 3.2×10-19×1.0 |
答:
(1)ab杆做匀速直线运动过程中,外力F的功率为1.28W;
(2)α射线源Q是钍核
294 63 |
295 56 |
256 60 |
258 58 |
4 2 |
(3)磁感应强度B2为1.6×10-4T.
点评:本题是电磁感应与力学、电路知识的综合,求解安培力,画出磁场中轨迹,由几何知识求轨迹半径是解题的两个关键.

练习册系列答案
相关题目
 如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R=0.4Ω,导轨上静止放置一质量为m=0.1kg、电阻r=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B=0.5T的匀强磁场中,磁场方向竖直向下,现用一个外力F沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末理想电压表的读数为0.2V.求
如图所示,光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R=0.4Ω,导轨上静止放置一质量为m=0.1kg、电阻r=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B=0.5T的匀强磁场中,磁场方向竖直向下,现用一个外力F沿水平方向拉杆,使之由静止起做匀加速运动并开始计时,若5s末理想电压表的读数为0.2V.求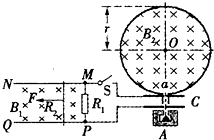 如图所示,光滑且足够长的平行导轨MN和PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R1=0.4Ω,导轨上静止放置一质量m=0.1kg,电阻R2=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止开始做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
如图所示,光滑且足够长的平行导轨MN和PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R1=0.4Ω,导轨上静止放置一质量m=0.1kg,电阻R2=0.1Ω的金属杆,导轨电阻忽略不计,整个装置处在磁感应强度B1=0.5T的匀强磁场中,磁场的方向竖直向下,现用一外力F沿水平方向拉杆,使之由静止开始做匀加速运动并开始计时,若5s末杆的速度为2.5m/s,求:
