题目内容
11. 在“验证机械能守恒定律”的实验中,打点计时器接在电压为6.0V、频率为50Hz的交流电源上,自由下落的重物质量为1.0kg,打下一条理想的纸带,数据如图所示,单位是cm,g取9.8m/s2,O、A之间有几个计数点未画出,求:
在“验证机械能守恒定律”的实验中,打点计时器接在电压为6.0V、频率为50Hz的交流电源上,自由下落的重物质量为1.0kg,打下一条理想的纸带,数据如图所示,单位是cm,g取9.8m/s2,O、A之间有几个计数点未画出,求:(1)打点计时器打下计数点B时,重物下落的速度vB=0.98 m/s
(2)从起点O到打下计数点B的过程中,重物的重力势能的减小量△Ep=0.49J,动能的增加量△Ek=0.48J.(保留两位小数)
分析 根据某段时间内的平均速度等于中间时刻的瞬时速度求出计数点B的速度,从而得出动能的增加量,根据下落的高度求出重力势能的减小量,结合动能增加量和重力势能减小量的关系判断机械能是否守恒.
解答 解:(1)利用匀变速直线运动的推论
vB=$\frac{0.0706-0.0314}{2×0.02}$=0.98m/s
(2)重力势能减小量△Ep=mgh=1×9.8×0.0501J=0.49 J.
EkB=$\frac{1}{2}$mvB2=0.48 J.
故答案为:(1)0.98;(2)0.49,0.48
点评 要知道重物带动纸带下落过程中能量转化的过程和能量守恒,重物带动纸带下落过程中,除了重力还受到阻力,从能量转化的角度,由于阻力做功,重力势能减小除了转化给了动能还有一部分转化给摩擦产生的内能.

练习册系列答案
相关题目
1.一个质子和一个中子聚变结合成一个氘核,同时辐射一个光子.已知质子、中子、氘核的质量分别为m1、m2、m3,普朗克常量为h,真空中的光速为c.下列说法正确的是( )
| A. | 核反应方程是${\;}_{1}^{1}H$+${\;}_{0}^{1}$n→${\;}_{1}^{3}$H+γ | |
| B. | 聚变反应中的质量亏损△m=m1+m2-m3 | |
| C. | 辐射出的光子的能量E=(m3-m1-m2)c2 | |
| D. | 光子的波长λ=$\frac{h}{({m}_{1}+{m}_{2}-{m}_{3}){c}^{2}}$ |
19. 甲、乙、丙三个小球分别位于如图所示的竖直平面内,甲乙在同一条竖直线上,甲丙在同一条水平线上,水平面上的P点在丙的正下方,在同一时刻甲乙丙开始运动,甲以水平速度v0做平抛运动,乙以相同的水平速度v0沿光滑水平面向右做匀速直线运动,丙做自由落体运动,则( )
甲、乙、丙三个小球分别位于如图所示的竖直平面内,甲乙在同一条竖直线上,甲丙在同一条水平线上,水平面上的P点在丙的正下方,在同一时刻甲乙丙开始运动,甲以水平速度v0做平抛运动,乙以相同的水平速度v0沿光滑水平面向右做匀速直线运动,丙做自由落体运动,则( )
 甲、乙、丙三个小球分别位于如图所示的竖直平面内,甲乙在同一条竖直线上,甲丙在同一条水平线上,水平面上的P点在丙的正下方,在同一时刻甲乙丙开始运动,甲以水平速度v0做平抛运动,乙以相同的水平速度v0沿光滑水平面向右做匀速直线运动,丙做自由落体运动,则( )
甲、乙、丙三个小球分别位于如图所示的竖直平面内,甲乙在同一条竖直线上,甲丙在同一条水平线上,水平面上的P点在丙的正下方,在同一时刻甲乙丙开始运动,甲以水平速度v0做平抛运动,乙以相同的水平速度v0沿光滑水平面向右做匀速直线运动,丙做自由落体运动,则( )| A. | 若甲乙丙三球同时相遇,一定发生在P点 | |
| B. | 若只有甲丙两球在水平面上相遇时,此时乙球不一定在P点 | |
| C. | 若只有甲乙两球在水平面上相遇,此时丙球还没落地 | |
| D. | 无论初速度v0大小如何,甲乙二球一定会相遇 |
6.一物体做匀变速直线运动,某时刻速度的大小为4m/s,1s后速度大小变为10m/s,在这1s内物体的以下说法错误的是( )
| A. | 平均速度的大小可能是7 m/s | B. | 位移的大小可能小于4 m | ||
| C. | 速度变化量大小可能小于4 m/s | D. | 加速度的大小可能小于10 m/s2 |
3.关于平抛物体的运动,下列说法中正确的是( )
| A. | 物体只受重力的作用,是a=g的匀变速曲线运动 | |
| B. | 初速度越大,物体在空中的飞行时间越长 | |
| C. | 平抛运动任一时刻的速度沿水平方向上的分量都相同 | |
| D. | 物体落地时的水平位移与抛出点的高度无关 |
1.在下列几个实例中,机械能守恒的是( )

| A. | 在平衡力作用下运动的物体 | |
| B. | 在光滑水平面上被细线拴住做匀速圆周运动的小球 | |
| C. | 在粗糙斜面上下滑的物体 | |
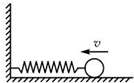
| D. | 如图所示,在光滑水平面上压缩弹簧过程中的小球 |
 如图所示,一个质子以初速度v0=5×106m/s射入一个由两块带电的平行金属板组成的区域.两板距离为20cm,金属板之间是匀强电场,电场强度为3×105V/m.质子质量为m=1.67×10-27kg,电荷量为q=1.60×10-19C.试求
如图所示,一个质子以初速度v0=5×106m/s射入一个由两块带电的平行金属板组成的区域.两板距离为20cm,金属板之间是匀强电场,电场强度为3×105V/m.质子质量为m=1.67×10-27kg,电荷量为q=1.60×10-19C.试求 物体质量m=6kg,在水平地面上受到与水平面成370角斜向上的拉力F=20N作用,物体以10m/s的速度作匀速直线运动,求力F撤去后物体还能运动多远?
物体质量m=6kg,在水平地面上受到与水平面成370角斜向上的拉力F=20N作用,物体以10m/s的速度作匀速直线运动,求力F撤去后物体还能运动多远?