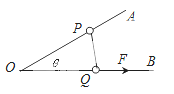
题目内容
如图所示,一个轻质直角形薄板ABC,AB=0.80m,AC="0.60" m,在A点固定一垂直于薄板平面的光滑转动轴,在薄板上D点固定一个质量为m=0.40kg的小球,现用测力计竖直向上拉住B点,使AB水平,如图(a),测得拉力F1=2.0N;再用测力计竖直向上拉住C点,使AC水平,如图(b),测得拉力F2=2.0N(g取10m/s2,sin37°=0.6,cos37°=0.8)。求:
(1)小球和转动轴的距离AD;
(2)在如图(a)情况下,将小球移动到BC边上距离A点最近处,然后撤去力F1,薄板转动过程中,AB边能转过的最大角度;
(3)在第(2)问条件下,薄板转动过程中,B点能达到的最大速度 。
。
(1)0.5m (2)74°(3)2.32m/s
解析试题分析:(1)设小球D距AC为x,距AB为y。
根据力矩平衡得:

所以 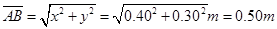
(2)设AD连线与AC边的夹角为θ,由几何关系可知 。根据机械能守恒定律得AD边转过的最大角度是2θ,所以AB边转过的最大角度是2θ=74°
。根据机械能守恒定律得AD边转过的最大角度是2θ,所以AB边转过的最大角度是2θ=74°
(3)根据机械能守恒定律,小球运动到最低点时,重力势能最小,动能最大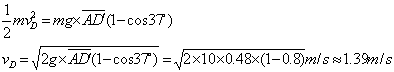
在转动过程中,薄板上各点角速度相同,所以
考点:本题考查了力矩平衡 机械能守恒定律

如图所示是古代农村中使用的一种舂米工具,O为固定轴,石块固定在A端,脚踏左端B可以使石块升高至P处,放开脚,石块会落下打击稻谷,若脚用力F,方向始终竖直向下,假如石块升到P处的过程中每时刻都处于平衡状态,则: ( )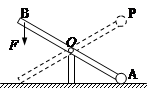
| A.F先变大后变小 | B.F的大小始终不变 |
| C.F的力矩始终不变 | D.F的力矩先变大后变小 |
下列关于使用和乘坐小汽车的说法,符合实际情况的是
| A.小汽车的司机和前排乘客必须系好安全带,这样可以防止惯性的危害 |
| B.小汽车车尾的导电链是为了防止静电积聚 |
| C.小汽车前大灯和挡风玻璃覆盖的偏振片能使驾驶员消除对面车灯的强烈炫光 |
| D.小汽车防雾灯一般为橙黄色光,橙黄色光的波长较短,穿透力弱 |
当作用在物体上的合外力不为零时( )
| A.物体的速度一定越来越大 | B.物体的速度一定越来越小 |
| C.物体的速度可能不变 | D.物体的运动状态一定变化 |
一汽车在路面情况相同的公路上直线行驶,下面关于车速、惯性、质量和滑行路程的讨论正确的是( )
| A.质量越大,它的惯性越大 |
| B.车速越大,它的惯性越大 |
| C.车速越大,刹车后滑行的路程不一定越长 |
| D.刹车后滑行的路程越长,惯性越大 |
意大利科学家伽利略在研究物体变速运动规律时,做了著名的“斜面实验”,他测量了铜球在较小倾角斜面上的运动情况,发现铜球做的是匀加速直线运动,且铜球加速度随斜面倾角的增大而增大,在当时的年代由于加速度增大而导致时间无法测定,于是他对大倾角情况进行了合理的外推,由此得出的结论是
| A.自由落体运动是一种匀加速直线运动 |
| B.力是使物体产生加速度的原因 |
| C.力不是维持物体运动的原因 |
| D.物体都具有保持原来运动状态的属性,即惯性 |
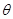 =30°的足够长的绝缘斜面,在斜面上P点的上方是光滑的,P点下方粗糙,整个斜面体处在一个交变的电磁场中,电、磁场的变化规律如图乙和丙所示,磁场方向以垂直纸面向外为正,而电场的方向以竖直向下为正,其中
=30°的足够长的绝缘斜面,在斜面上P点的上方是光滑的,P点下方粗糙,整个斜面体处在一个交变的电磁场中,电、磁场的变化规律如图乙和丙所示,磁场方向以垂直纸面向外为正,而电场的方向以竖直向下为正,其中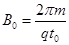 ,
,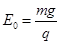 ,现有一个可视为质点、带负电的小物块(其质量为
,现有一个可视为质点、带负电的小物块(其质量为 、带电量大小为
、带电量大小为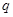 ),从t=0时刻由静止开始从A点沿斜面下滑,在t=3t0时刻刚好到达斜面上的P点,在以后运动过程中的某时刻开始,物块运动的速率保持不变.若已知斜面粗糙部分与物块间的动摩擦因素为
),从t=0时刻由静止开始从A点沿斜面下滑,在t=3t0时刻刚好到达斜面上的P点,在以后运动过程中的某时刻开始,物块运动的速率保持不变.若已知斜面粗糙部分与物块间的动摩擦因素为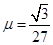 ,求:
,求: