Question

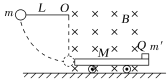
【题目】如图所示，将带电荷量Q＝＋0.3 C、质量m′＝0.3 kg的滑块放在小车的水平绝缘板的右端，小车的质量M＝0.5 kg，滑块与绝缘板间的动摩擦因数μ＝0.4，小车的绝缘板足够长，它们所在的空间存在磁感应强度B＝20 T的水平方向的匀强磁场(垂直于纸面向里)。开始时小车静止在光滑水平面上，一摆长L＝1.25 m、质量m＝0.15 kg的摆从水平位置由静止释放，摆到最低点时与小车相撞，碰撞后摆球恰好静止，g取10 m/s2。求：

(1)与小车碰撞前摆球到达最低点时对摆线的拉力；

(2)摆球与小车的碰撞过程中系统损失的机械能ΔE；

(3)碰撞后滑块最终悬浮时的速度。

Answer 1

【答案】(1)4.5 N　方向竖直向下　(2)1.31 J(3)0.5 m/s　方向水平向右

【解析】

（1）摆球下落过程，由动能定理有mgL＝mv2，

解得v＝5 m/s，

摆球在最低点时，由牛顿第二定律得T－mg＝m，

解得T＝4.5 N，

由牛顿第三定律可知摆球对摆线的拉力T′＝4.5 N，方向竖直向下。

（2）摆球与小车碰撞瞬间，摆球与小车组成的系统动量守恒，以水平向右为正方向，

有mv＝Mv1＋0，

解得v1＝1.5 m/s，

由能量守恒定律，有ΔE＝mv2－Mv12＝1.31 J。

（3）滑块悬浮瞬间，满足F洛′＝Qv2′B＝m′g，

解得v2′＝0.5 m/s。