题目内容
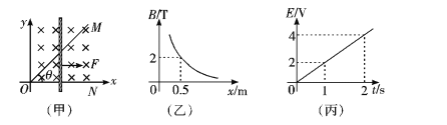
【题目】如图(甲)所示,水平面内的直角坐标系的第一象限有磁场分布,方向垂直于水平面向下,磁感应强度沿y轴方向没有变化,与x轴的关系如图(乙)所示, 图线是双曲线(坐标轴是渐近线);顶角θ=45°的光滑金属长导轨MON固定在水平面内,ON与x轴重合,一根与ON垂直的长导体棒在水平向右的外力作用下沿导轨MON向右滑动,导体棒在滑动过程中始终与与导轨良好接触。已知t=0时,导体棒位于顶点O处;导体棒的质量为m=2kg,OM,ON接触处O点的接触电阻为R=0.5Ω,其余电阻不计;回路电动势E与时间t的关系如图(丙)所示,图线是过原点的直线。求:
(1)t=2s时流过导体棒的电流I2的大小;
(2)导体棒滑动过程中水平外力F(单位:N)与横坐标x(单位:m)的关系式。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】(1)根据E-t图象中的图线是过原点的直线特点,可得到t=2s时金属棒产生的感应电动势为:E=4V
由欧姆定律得:![]()
(2)因θ=45°,可知任意t时刻回路中导体棒有效切割长度 L=x
再根据B-x图象中的图线是双曲线特点有:E=BLv=(Bx)v,
由图2可知,Bx=1(Tm).
由图1知:E与时间成正比,有 E=2t(V)
由以上三式得:v=2t(m/s)
可知导体棒的运动是匀加速直线运动,加速度 a=2m/s2,
又有:F安=BIL=BIx=(Bx)I,且I也与时间成正比
再根据牛顿第二定律有:F-F安=ma
又x=![]() at2
at2
联立解得:F=(4+4![]() )N
)N

练习册系列答案
相关题目