题目内容
如图所示，光滑曲面AB与水平面BC平滑连接于B点，BC右端连接内壁光滑、半径为r的
细圆管CD，管口D端正下方直立一根劲度系数为k的轻弹簧，轻弹簧下端固定，上端恰好与管口D端齐平。质量为m的小球在曲面上距BC的高度为2r处从静止开始下滑，进入管口C端时与管壁间恰好无作用力，通过CD后压缩弹簧，在压缩弹簧过程中速度最大时弹簧的弹性势能为EP，已知小球与BC间的动摩擦因数μ=0.5。求：
（1）小球达到B点时的速度大小vB；
（2）水平面BC的长度s；
（3）在压缩弹簧过程中小球的最大速度vm 。
（1）由机械能守恒得
mg2r=
mvB2
解得vB=2
（2）由mg=m
得vC=
由动能定理得
mg2r－μmgs=mvC2
解得s=3r
（3）设在压缩弹簧过程中小球速度最大时离D端的距离为x，则有
kx=mg
得x= 
由功能关系得 mg(r+x) -EP = mvm2-mvC2
得 vm=
如图所示，光滑曲面上方有一固定的带电量为+Q 的点电荷，现有一带电量为+q的金属小球（可视为质点），在A点以初速度v0射入后始终沿着曲面运动，小球与曲面相互绝缘，则（ ）
（2011?周口模拟）【物理-选修3-5】
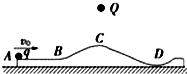如图所示，光滑曲面上方有一固定的带电量为+Q的点电荷，现有一带电量为+q的金属小球（可视为质点），在A点以初速度v0射入后始终沿着曲面运动，小球与曲面相互绝缘，则（ ）| A、小球从A点运动到B点过程中，速度逐渐增大 | B、小球从A点到C点过程中，重力势能的增加量小于其动能的减少量 | C、小球在C点时受到+Q的库仑力最大，所以对曲面的压力最大 | D、小球在曲面上运动过程中，机械能始终守恒 |
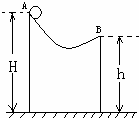如图所示，光滑曲面的两端A、B离地面的高度分别为H和h，一小球自A端由静止释放沿曲面下滑并经过B端飞出落地，则小球经过B端时的速率与刚落地时的速率之比为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
