Question

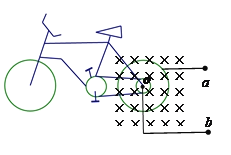
【题目】如图所示，空间内有方向垂直纸面(竖直面)向里的有界匀强磁场区域Ⅰ、Ⅱ，磁感应强度大小未知．区域Ⅰ内有竖直向上的匀强电场，区域Ⅱ内有水平向右的匀强电场，两区域内的电场强度大小相等．现有一质量m＝0.01 kg、电荷量q＝0.01 C的带正电滑块从区域Ⅰ左侧与边界MN相距L＝2 m的A点以v0＝5 m/s的初速度沿粗糙、绝缘的水平面向右运动，进入区域Ⅰ后，滑块立即在竖直平面内做匀速圆周运动，在区域Ⅰ内运动一段时间后离开磁场落回A点．已知滑块与水平面间的动摩擦因数μ＝0.225，重力加速度g＝10 m/s2.

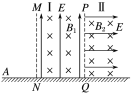
(1)求匀强电场的电场强度大小E和区域Ⅰ中磁场的磁感应强度大小B1；

(2)求滑块从A点出发到再次落回A点所经历的时间t；

(3)若滑块在A点以v0′＝9 m/s的初速度沿水平面向右运动，当滑块进入区域Ⅱ后恰好能做匀速直线运动，求有界磁场区域Ⅰ的宽度d及区域Ⅱ内磁场的磁感应强度大小B2.

Answer 1

【答案】(1)10 V/m　6.4 T (2)() s (3)m　T

【解析】

（1）小球进入复合场区域后，小球立即在竖直平面内做匀速圆周运动，说明重力与电场力的大小相等，方向相反；A到N的过程中根据牛顿第二定律可求出小球到达N点的速度。小球离开磁场后做平抛运动，将运动分解，即可求出下落的高度，然后结合几何关系由于洛伦兹力提供向心力的公式即可求出磁感应强度；

（2）小球在AN之间做减速运动，由运动学的公式求出时间；粒子在磁场中做匀速圆周运动，由周期公式即可求出粒子在磁场中运动的时间，根据平抛运动的规律求平抛运动的时间，最后求和；

（3）A到N的过程中摩擦力做功，由动能定理即可求出小球到达N点的速度。小球进入区域Ⅱ后恰好能沿直线运动，说明小球受到的合外力为0，受力分析即可求出小球的速度，结合动能定理即可求出有界磁场区域Ⅰ的宽度d及区域Ⅱ的磁感应强B2的大小。

(1)滑块在区域Ⅰ内做匀速圆周运动时，重力与电场力平衡，则有mg＝qE

解得E＝＝10 V/m

滑块在AN间运动时，设水平向右的方向为正方向，由牛顿第二定律可得：

a＝－μg＝－2.25 m/s2

由运动公式可得v2－v02＝2aL

代入数据得v＝4 m/s

平抛运动过程满足L＝vt3；2r＝

做圆周运动满足qvB1＝m

联立方程求解得B1＝6.4 T

(2)滑块在AN间的时间

在磁场中做匀速圆周运动的时间

平抛运动的时间t3＝＝0.5 s

总时间为t＝t1＋t2＋t3＝s

(3)设滑块进入磁场时的速度为v′，满足

－μmgL＝mv′2－mv0′2

代入数据得v′＝6m/s

滑块在区域Ⅱ中做直线运动时，合力一定为0，由平衡方程知qv′B2＝mg

解得B2＝T

滑块离开磁场区域Ⅰ时的速度方向一定与水平成45°角．由几何关系知当滑块在区域Ⅰ中做匀速圆周运动时有

B1qv′＝

解得

由题意知d＝r·sin 45°＝m