题目内容
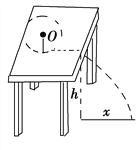
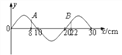
【题目】如图所示.,现有一块表面水平的木板,被放在光滑的水平地面上。它的右端与墙之间有一段距离,其长度L为0.08m。另有一小物块以2m/s 的初速度v0从木板的左端滑上它.已知木板和小物块的质量均为1kg,小物块与木板之间的动摩擦因数μ=0.1,木板足够长使得在以后的运动过程中小物块始终不与墙接触,木板与墙碰后木板以原速率反弹,碰撞时间极短可忽略,取g=10m/s2。求:

(1)木板第一次与墙碰撞时的速度;
(2)从小物块滑上木板到二者达到共同速度时,木板与墙碰撞的次数和所用的时间;
(3)达到共同速度时木板右端与墙之间的距离.
【答案】(1)4m/s(2)2;1.8s(3)0.06m
【解析】试题分析:(1)物块滑上木板后,在摩擦力作用下,木板从静止开始做匀加速运动,设木板加速度为a,经历时间T后与墙第一次碰撞,碰撞时的速度为![]()
则![]() ,解得
,解得![]() ①
①
![]() ②,
②, ![]() ③
③
联立①②③解得![]() ,
, ![]() ④
④
(2)在物块与木板两者达到共同速度前,在每两次碰撞之间,木板受到物块对它的摩擦力作用而做加速度恒定的匀减速直线运动,因而木板与墙相碰后将返回至初态,所用时间也为T.
设在物块与木板两者达到共同速度v前木板共经历n次碰撞,则有: ![]() ⑤
⑤
式中△t是碰撞n次后木板从起始位置至达到共同速度时所需要的时间.
由于最终两个物体一起以相同的速度匀速前进,故⑤式可改写为![]() ⑥
⑥
由于木板的速率只能处于0到![]() 之间,故有
之间,故有![]() ⑦
⑦
求解上式得![]()
由于n是整数,故有n=2⑧
由①⑤⑧得: ![]() ⑨;
⑨; ![]() ⑩
⑩
从开始到物块与木板两者达到共同速度所用的时间为: ![]() (11)
(11)
即从物块滑上木板到两者达到共同速度时,木板与墙共发生三次碰撞,所用的时间为1.8s.
(3)物块与木板达到共同速度时,木板与墙之间的距离为![]() (12)
(12)
联立①与(12)式,并代入数据得![]()
即达到共同速度时木板右端与墙之间的距离为0.06m.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案