题目内容
19. 如图所示,竖直虚线MN、PQ将两竖直挡板A、B间空间分成等间距的三区域Ⅰ、Ⅱ、Ⅲ,在区域Ⅰ内有一与水平线OO1成37°角的光滑绝缘斜面AC(C是MN与OO1的交点),区域Ⅱ内有竖直向上的匀强电场,区域Ⅲ内存在水平向左的匀强电场,两区域电场强度均未知.现有一电荷量为q、质量为m的带电滑块(可看作质点)从左挡板的A点由静止释放,从C点进入区域Ⅱ后恰好能垂直PQ进入区域Ⅲ,最后滑块恰好与挡板B相切于D点(没画出),已知各区域宽均为L,重力加速度为g,滑块运动中电荷量不变,求:
如图所示,竖直虚线MN、PQ将两竖直挡板A、B间空间分成等间距的三区域Ⅰ、Ⅱ、Ⅲ,在区域Ⅰ内有一与水平线OO1成37°角的光滑绝缘斜面AC(C是MN与OO1的交点),区域Ⅱ内有竖直向上的匀强电场,区域Ⅲ内存在水平向左的匀强电场,两区域电场强度均未知.现有一电荷量为q、质量为m的带电滑块(可看作质点)从左挡板的A点由静止释放,从C点进入区域Ⅱ后恰好能垂直PQ进入区域Ⅲ,最后滑块恰好与挡板B相切于D点(没画出),已知各区域宽均为L,重力加速度为g,滑块运动中电荷量不变,求:(1)区域Ⅱ中电场强度E1的大小.
(2)区域Ⅲ中电场强度E2的大小.
(3)O1D的长.
分析 (1)在区域Ⅱ内,小球做匀变速曲线运动,将其运动进行正交分解:水平方向匀加速直线运动,竖直方向做匀减速直线运动,两个分运动时间相等,由平均速度表示两个方向的分位移,求出小球离开区域Ⅱ时偏转的距离,由运动学公式即可求得;
(2)区域III内滑块在水平方向做匀减速直线运动且挡板B时速度恰好为0,在竖直方向做自由落体运动
(3)由(1)(2)即可求得位移
解答 解:(1)区域I内,有动能定理由$mgtan37°=\frac{1}{2}{mv}_{C}^{2}$
滑块恰好能垂直PQ进入区域III
区域II内,滑块在水平方向上左匀速直线运动,由L=vCcos37°•t1
在竖直方向做匀减速运动,由${v}_{C}sin37°=\frac{q{E}_{1}-mg}{m}$
在竖直方向发生的位移${y}_{1}={v}_{C}sin37°•{t}_{1}-\frac{1}{2}•{\frac{q{E}_{1}-mg}{m}t}_{1}^{2}$
联立解得${E}_{1}=\frac{43mg}{25q}$
${y}_{1}=\frac{3}{8}L$
(2)区域III内滑块在水平方向做匀减速直线运动且挡板B时速度恰好为0,在竖直方向做自由落体运动,由${v}_{C}=cos37°=\frac{q{E}_{2}}{m}{t}_{2}$
L=$\frac{{v}_{C}cos37°}{2}{t}_{2}$
${y}_{2}=\frac{1}{2}{gt}_{2}^{2}$
联立解得${E}_{2}=\frac{12mg}{25q}$
${y}_{2}=\frac{25}{12}L$
(3)O1D的长度为$L′={y}_{1}+{y}_{2}=\frac{59L}{24}$
答:(1)区域Ⅱ中电场强度E1的大小为$\frac{43mg}{25q}$.
(2)区域Ⅲ中电场强度E2的大小为$\frac{43mg}{25q}$.
(3)O1D的长为$\frac{59L}{24}$.
点评 本题主要考查了带电粒子在混合场中运动的问题,要求同学们能正确分析粒子的受力情况,再通过受力情况分析粒子的运动情况,画出运动轨迹图,根据几何知识及圆周运动基本公式解答,难度较大

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示,半径和动能都相等的两个小球相向而行.甲球质量m甲大于乙球质量m乙,水平面是光滑的,两球做对心碰撞以后的运动情况可能是下述哪些情况( )
如图所示,半径和动能都相等的两个小球相向而行.甲球质量m甲大于乙球质量m乙,水平面是光滑的,两球做对心碰撞以后的运动情况可能是下述哪些情况( )| A. | 甲球速度为零,乙球速度不为零 | B. | 乙球速度为零,甲球速度不为零 | ||
| C. | 两球速度都为零 | D. | 两球都以各自原来的速率反向运动 |
| A. | 不变 | B. | 减小 | C. | 增加 | D. | 先减小后增加 |
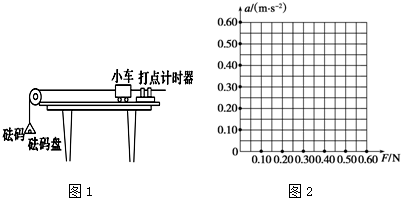
(1)下列说法中正确的是CD
A.在探究加速度与质量的关系时,应改变拉力的大小
B.在探究加速度与外力的关系时,应该改变小车的质量
C.在探究加速度a与质量m的关系时,为了更直观判断二者间的关系,应作出a-1/m图象
D.当小车的质量远大于砝码盘和砝码的总质量时,才能近似认为细线对小车的拉力大小等于砝码盘和砝码的总重力大小
(2)某同学测得小车的加速度a和拉力F的数据如表所示.(小车质量保持不变)
| F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| a/(m•s-2) | 0.10 | 0.20 | 0.28 | 0.40 | 0.52 |
②分析①中a-F图象不过原点的原因可能是没有平衡摩擦力或平衡摩擦力时木板倾角太小.
 如图所示,竖直放置在水平面上的轻质弹簧上放着质量为2kg的物体A,处于静止状态.若将一个质量为3kg的物体B竖直向下轻放在A上的一瞬间,则B对A的压力大小为(取g=10m/s2)( )
如图所示,竖直放置在水平面上的轻质弹簧上放着质量为2kg的物体A,处于静止状态.若将一个质量为3kg的物体B竖直向下轻放在A上的一瞬间,则B对A的压力大小为(取g=10m/s2)( )| A. | 30N | B. | 0N | C. | 15N | D. | 12N |
| A. | 日光灯的镇流器为日光灯的点亮提供瞬时高压 | |
| B. | 示波器面板上的Y增益旋钮用来调节图象的竖直位置 | |
| C. | 变压器的高压线圈用较粗的导线绕制,低压线圈用较细的导线绕制 | |
| D. | 某交变电流的频率为50 Hz,则该交流电电流的方向在1秒内改变50次 |
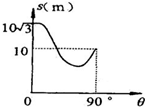 有一个斜面,其底边固定且水平,斜面倾角θ在0-90°内变化,一质量为m=1kg的物体以某一初速度自斜面底端沿斜面上滑,在斜面上滑动时的最大位移s随θ角变化的规律如图所示.则当θ=30°时,物体上滑的最大位移S和此过程中克服摩擦力所做的功W分别为(g取10m/s2)( )
有一个斜面,其底边固定且水平,斜面倾角θ在0-90°内变化,一质量为m=1kg的物体以某一初速度自斜面底端沿斜面上滑,在斜面上滑动时的最大位移s随θ角变化的规律如图所示.则当θ=30°时,物体上滑的最大位移S和此过程中克服摩擦力所做的功W分别为(g取10m/s2)( )| A. | S=10$\sqrt{3}$m | B. | S=10m | C. | W=50$\sqrt{3}$J | D. | W=50J |
| A. | 100个钚239原子核储存2.41万年,还能剩下50个 | |
| B. | 铀238变成钚239过程中,其中的一个核反应方程是:${\;}_{92}^{238}$U+${\;}_{0}^{1}$n→${\;}_{92}^{239}$U | |
| C. | 镎239能发生β衰变,产生的β粒子(电子)是核外电子脱离原子核的束缚形成的 | |
| D. | 快中子反应堆虽然释放能量,但没有质量亏损 |
 如图所示,矩形闭合导体线圈,在外力作用下,匀速向右通过宽为d的匀强磁场,设穿过线圈的磁通量为Φ,感应电动势为E,线圈所受磁场力为F,通过线圈的电荷量为Q,则图中正确的是( )
如图所示,矩形闭合导体线圈,在外力作用下,匀速向右通过宽为d的匀强磁场,设穿过线圈的磁通量为Φ,感应电动势为E,线圈所受磁场力为F,通过线圈的电荷量为Q,则图中正确的是( )


