题目内容
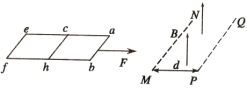
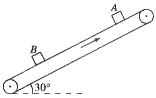
【题目】如图所示，足够长的传送带与水平面的夹角θ=30°，传送带顺时针匀速运动的速度大小v0=2m/s，物块A的质量m1=1kg，与传送带间的动摩擦因数
；物块B的质量m2=3kg，与传送带间的动摩擦因数
。将两物块由静止开始同时在传送带上释放，经过一段时间两物块发生碰撞并粘在一起，碰撞时间极短。开始释放时两物块间的距离L=13m。已知重力加速度g=10m/s2，A、B相对传送带滑动时会留下浅痕，最大静摩擦力等于滑动摩擦力。求：
(1)两物块刚释放后各自加速度的大小；
(2)两物块释放后经过多长时间发生碰撞；
(3)传送带上痕迹的长度。
【答案】(1)2m/s2，1m/s2；(2)3s；(3)23m
【解析】
(1)A沿斜面向下运动时
得
al=2m/s2
B沿斜面向上加速运动时
得
a2=1m/s2
(2)由v0=a1t0 得
t0=2s
即经过2s时两物块还没相撞
得
t=3s
经过3s两物块相撞
(3)两物块相撞前，A的速度大小
v1=a1t
碰撞过程中由动量守恒定律
m1v1－m2v2=(m1+m2)v
得
v=0
碰撞后，对两物块受力分析有
a3=0.25m/s2
方向沿传送带向上
由v0=a3tl 得
t1=8s
即碰撞后经过8s两物块相对传送带静止。
设碰撞前物块A相对传送带的位移为x1
碰撞后，两物块相对传送带的位移x2
分析可得，痕迹长度为
l=x1+x2=23m
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
