题目内容
一个质量为m的物体，在几个与平面平行的力的作用下静止在一水平面上，现将其中一个向东的力从F减小到
F，其他的力未发生变化，那么物体在时间t内的位移将是下面所列各项的哪一个（ ）
| 1 |
| 4 |
分析：先根据共点力平衡条件求出变化后的合力，再求出加速度，根据位移时间关系公式求位移．
解答：解：刚开始合力为零，除力F外的其余力的合力大小为F，方向与F反向，故将力F减小为
F时，合力为
F，方向向西；
根据牛顿第二定律
a=
方向向西；
根据位移时间关系公式
s=
at2=
故选D．
| 1 |
| 4 |
| 3 |
| 4 |
根据牛顿第二定律
a=
| 3F |
| 4m |
根据位移时间关系公式
s=
| 1 |
| 2 |
| 3Ft2 |
| 8m |
故选D．
点评：本题关键先求出合力，然后求出加速度，最后根据位移时间关系公式求位移．
练习册系列答案
相关题目
（2011?徐汇区模拟）如图（a）所示，在倾角为37°的斜面上，一个质量为m的物体A在沿斜面向下的不同的恒定拉力F作用下从静止开始运动，设沿斜面向下的方向为正方向，物体A的加速度a与拉力F的关系如图（b）所示，则物体A的质量m为
如图所示，一个粗糙的水平转台以角速度ω匀速转动，转台上有一个质量为m的物体，物体与转台问用长L的绳连接着，此时物体与转台处于相对静止，设物体与转台间的动摩擦因数为μ，现突然制动转台，则（ ）
（2009?丰台区模拟）如图所示，一个质量为m的物体沿固定斜面匀速滑下，以下说法正确的是（ ）
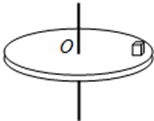如图所示，一圆盘可绕通过其中心且垂直于盘面的竖直轴转动，盘上距中心r处放置一个质量为m的物体，物体与盘面间滑动摩擦因数为μ，重力加速度为g．一段时间内观察到圆盘以角速度ω做匀速转动，物体随圆盘一起（相对静止）运动．这段时间内（ ）| A、物体受到圆盘对它的摩擦力，大小一定为μmg，方向与物体线速度方向相同 | B、物体受到圆盘对它的摩擦力，大小一定为mω2r，方向指向圆盘中心 | C、物体受到圆盘对它的摩擦力，大小可能小于μmg，方向指向圆盘中心 | D、物体受到圆盘对它的摩擦力，大小可能小于mω2r，方向背离圆盘中心 |