题目内容
 如图所示,水平传送带A、B两端点相距x=4m,以v=2m/s的速度(始终保持不变)顺时针运转,今将一质量为100g小煤块(可视为质点)无初速度地轻放至A点处,已知小煤块与传送带间的动摩擦因数为0.4,g取10m/s2.由于小煤块与传送带之间有相对滑动,会在传送带上留下划痕,则小煤块从A运动到B的过程中
如图所示,水平传送带A、B两端点相距x=4m,以v=2m/s的速度(始终保持不变)顺时针运转,今将一质量为100g小煤块(可视为质点)无初速度地轻放至A点处,已知小煤块与传送带间的动摩擦因数为0.4,g取10m/s2.由于小煤块与传送带之间有相对滑动,会在传送带上留下划痕,则小煤块从A运动到B的过程中(1)小煤块从A运动到B的时间是多少?
(2)划痕的长度?
(3)产生的热量?
(4)传送物体电动机多做的功?
分析:(1)小煤块放上传送带先做匀加速直线运动,然后做匀速直线运动,根据运动学公式结合牛顿第二定律求出小煤块从A运动到B的时间.
(2)分别求出在煤块匀加速直线运动阶段传送带的位移和煤块的位移,两者位移之差即为划痕的长度.
(3)产生的热量为滑动摩擦力所做的功;
(4)传送物体电动机多做的功是物块产生的动能与及产生了热量之和.
(2)分别求出在煤块匀加速直线运动阶段传送带的位移和煤块的位移,两者位移之差即为划痕的长度.
(3)产生的热量为滑动摩擦力所做的功;
(4)传送物体电动机多做的功是物块产生的动能与及产生了热量之和.
解答:解:(1、2)小煤块先加速后匀速,根据牛顿第二定律得;a=
=μg=4m/s2
加速阶段的时间:t1=
=
=0.5 s,
小煤块位移为:x1=
at12=
×4×0.25=0.5 m,
传送带位移为:x2=vt1=2×0.5=1 m,
所以划痕长度是△x=x2-x1=0.5 m;
小煤块匀速阶段的时间为:t2=
=
=1.75 s,
故小煤块从A运动到B的时间是:t=t1+t2=2.25 s.
(3)产生的热量Q=f△x=μmg△x=0.4×0.1×10×0.5=0.2J
(4)传送物体电动机多做的功是物块产生的动能与及产生了热量之和,则
W=
mv2+Q=
×0.1×4+0.2=0.4J
答:(1)所用的时间为2.25s.
(2)划痕的长度为0.5m;
(3)产生的热量为0.2J;
(4)传送物体电动机多做的功为0.4J.
| μmg |
| m |
加速阶段的时间:t1=
| v |
| a |
| 2 |
| 4 |
小煤块位移为:x1=
| 1 |
| 2 |
| 1 |
| 2 |
传送带位移为:x2=vt1=2×0.5=1 m,
所以划痕长度是△x=x2-x1=0.5 m;
小煤块匀速阶段的时间为:t2=
| x-x1 |
| v |
| 4-0.5 |
| 2 |
故小煤块从A运动到B的时间是:t=t1+t2=2.25 s.
(3)产生的热量Q=f△x=μmg△x=0.4×0.1×10×0.5=0.2J
(4)传送物体电动机多做的功是物块产生的动能与及产生了热量之和,则
W=
| 1 |
| 2 |
| 1 |
| 2 |
答:(1)所用的时间为2.25s.
(2)划痕的长度为0.5m;
(3)产生的热量为0.2J;
(4)传送物体电动机多做的功为0.4J.
点评:分析清楚物体运动的过程,先是匀加速直线运动,后是匀速直线运动,分过程应用运动规律求解即可,尤其是注意分析摩擦力的变化情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
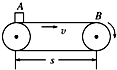 如图所示,水平传送带长为s,以速度v始终保持匀速运动,质量为m的货物无初速放到A点,货物运动到B点时恰达到速度v,货物与皮带间的动摩擦因数为μ,当货物从A点运动到B点的过程中,以下说法正确的是( )
如图所示,水平传送带长为s,以速度v始终保持匀速运动,质量为m的货物无初速放到A点,货物运动到B点时恰达到速度v,货物与皮带间的动摩擦因数为μ,当货物从A点运动到B点的过程中,以下说法正确的是( )A、摩擦力对物体做功为
| ||
| B、摩擦力对物体做功为μmgs | ||
| C、传送带克服摩擦力做功为μmgs | ||
| D、因摩擦而生的热能为2μmgs |
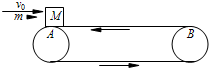 (2007?淮安模拟)如图所示,水平传送带AB长l=8.3m,质量为M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动(传送带的传送速度恒定),木块与传送带间的动摩擦因数μ=0.5.当木块运动至最左端A点时,一颗质量为m=20g的子弹以v0=300m/s水平向右的速度正对射入木块并穿出,穿出速度v=50m/s,以后每隔1s就有一颗子弹射向木块,设子弹射穿木块的时间极短,且每次射入点各不相同,g取10m/s2.求:
(2007?淮安模拟)如图所示,水平传送带AB长l=8.3m,质量为M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动(传送带的传送速度恒定),木块与传送带间的动摩擦因数μ=0.5.当木块运动至最左端A点时,一颗质量为m=20g的子弹以v0=300m/s水平向右的速度正对射入木块并穿出,穿出速度v=50m/s,以后每隔1s就有一颗子弹射向木块,设子弹射穿木块的时间极短,且每次射入点各不相同,g取10m/s2.求: 用如图所示的水平传送带AB和斜面BC将货物运送到斜面的顶端.传送带AB的长度L=11m,上表面保持匀速向右运行,运行的速度v=12m/s.传送带B端靠近倾角θ=37?的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔△t=1.0s将一个质量m=10kg的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的
用如图所示的水平传送带AB和斜面BC将货物运送到斜面的顶端.传送带AB的长度L=11m,上表面保持匀速向右运行,运行的速度v=12m/s.传送带B端靠近倾角θ=37?的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔△t=1.0s将一个质量m=10kg的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的 如图所示,水平传送带长为s,以速度v始终保持匀速运动,把质量为m的货物放到A点,货物与皮带间的动摩擦因数为μ,当货物从A点运动到B点的过程中,摩擦力对货物做的功可能( )
如图所示,水平传送带长为s,以速度v始终保持匀速运动,把质量为m的货物放到A点,货物与皮带间的动摩擦因数为μ,当货物从A点运动到B点的过程中,摩擦力对货物做的功可能( ) 如图所示,水平传送带以恒定速度5m/s沿图示方向运动,地面上PQ区间有垂直纸面向里的匀强磁场,B=1T,一质量为0.01kg的带正电0.05C的小物体从磁场左方某处无初速释放到传送带上,若物体与传送带间的动摩擦因数μ=0.2,那么,欲使小物体能匀速通过磁场区域,它释放时离磁场左边界P的距离应为多大?(g取10m/s2)
如图所示,水平传送带以恒定速度5m/s沿图示方向运动,地面上PQ区间有垂直纸面向里的匀强磁场,B=1T,一质量为0.01kg的带正电0.05C的小物体从磁场左方某处无初速释放到传送带上,若物体与传送带间的动摩擦因数μ=0.2,那么,欲使小物体能匀速通过磁场区域,它释放时离磁场左边界P的距离应为多大?(g取10m/s2)