题目内容
7.关于黄光和蓝光,下列说法中正确的是( )| A. | 黄光光子的能量比蓝光光子的能量小 | |
| B. | 在真空中黄光的传播速度较蓝光的小 | |
| C. | 从玻璃射向空气,黄光的临界角比蓝光的临界角小 | |
| D. | 用同一装置做双缝干涉实验,黄光的条纹间距比蓝光的条纹间距小 |
分析 根据光的频率大小,波长的大小,结合v=$\frac{c}{n}$比较光在玻璃中的速度大小;并根据干涉条纹间距公式$△x=\frac{L}{d}λ$;最后根据$sinC=\frac{1}{n}$,确定临界角与折射率的大小有关系,即可一一判定求解.
解答 解:A、因黄光光子的频率比蓝光光子的频率小,根据E=hγ,则有黄光光子的能量比蓝光光子的能量小,故A正确.
B、任何光在真空中,传播速度都相同.故B错误.
C、从玻璃射向空气,根据$sinC=\frac{1}{n}$,可知,折射率越大的,临界角越小,因黄光的折射率比蓝光小,因此黄光的临界角比蓝光的临界角大.故C错误.
D、根据干涉条纹间距公式$△x=\frac{L}{d}λ$,因黄光的波长比蓝光大,则有黄光的条纹间距比蓝光的条纹间距大,故D错误.
故选:A.
点评 解决本题的突破口在于确定两光的频率高低,并知道折射率、频率、波长、在介质中的速度之间的大小关系,最后掌握干涉条纹间距公式的应用.

练习册系列答案
相关题目
18.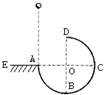 固定在竖直平面的光滑圆弧轨道ABCD,其A点与圆心O等高,D点为轨道最高点,DB为竖直直线,AC为水平线,AE为水平面,如图所示.今使小球自A点正上方某处由静止释放,且从A点进入圆轨道,只要适当调节释放点的高度,总能使球通过最高点D,则小球通过D点后( )
固定在竖直平面的光滑圆弧轨道ABCD,其A点与圆心O等高,D点为轨道最高点,DB为竖直直线,AC为水平线,AE为水平面,如图所示.今使小球自A点正上方某处由静止释放,且从A点进入圆轨道,只要适当调节释放点的高度,总能使球通过最高点D,则小球通过D点后( )
 固定在竖直平面的光滑圆弧轨道ABCD,其A点与圆心O等高,D点为轨道最高点,DB为竖直直线,AC为水平线,AE为水平面,如图所示.今使小球自A点正上方某处由静止释放,且从A点进入圆轨道,只要适当调节释放点的高度,总能使球通过最高点D,则小球通过D点后( )
固定在竖直平面的光滑圆弧轨道ABCD,其A点与圆心O等高,D点为轨道最高点,DB为竖直直线,AC为水平线,AE为水平面,如图所示.今使小球自A点正上方某处由静止释放,且从A点进入圆轨道,只要适当调节释放点的高度,总能使球通过最高点D,则小球通过D点后( )| A. | 一定会落到水平面AE上 | B. | 可能从A点又进入圆轨道 | ||
| C. | 可能撞在圆轨道AB间某位置 | D. | 可能从D点自由下落 |
15. 如图所示,是一名登山运动员的攀登陡峭雪壁的情形,如果认为峭壁的平面是竖直的平面,冰面是光滑的,腿与峭壁面是垂直的,轻绳与壁面的夹角为30°,运动员重为80kg.则细绳给人的张力大小T( )
如图所示,是一名登山运动员的攀登陡峭雪壁的情形,如果认为峭壁的平面是竖直的平面,冰面是光滑的,腿与峭壁面是垂直的,轻绳与壁面的夹角为30°,运动员重为80kg.则细绳给人的张力大小T( )
 如图所示,是一名登山运动员的攀登陡峭雪壁的情形,如果认为峭壁的平面是竖直的平面,冰面是光滑的,腿与峭壁面是垂直的,轻绳与壁面的夹角为30°,运动员重为80kg.则细绳给人的张力大小T( )
如图所示,是一名登山运动员的攀登陡峭雪壁的情形,如果认为峭壁的平面是竖直的平面,冰面是光滑的,腿与峭壁面是垂直的,轻绳与壁面的夹角为30°,运动员重为80kg.则细绳给人的张力大小T( )| A. | T=$\frac{800\sqrt{3}}{3}$N | B. | T=800N | C. | T=$\frac{1600\sqrt{3}}{3}$N | D. | T=1600N |
2. 如图所示为江西艺人茅荣荣,他以7个半小时内连续颠球5万次成为新的吉尼斯纪录创造者,而这个世界纪录至今无人超越.若足球用头顶起,某一次上升高度为80cm,足球的重量为400g,与头顶作用时间△t为0.1s,则足球本次在空中的运动时间;足球给头部的作用力大小.(空气阻力不计,g=10m/s2)( )
如图所示为江西艺人茅荣荣,他以7个半小时内连续颠球5万次成为新的吉尼斯纪录创造者,而这个世界纪录至今无人超越.若足球用头顶起,某一次上升高度为80cm,足球的重量为400g,与头顶作用时间△t为0.1s,则足球本次在空中的运动时间;足球给头部的作用力大小.(空气阻力不计,g=10m/s2)( )
 如图所示为江西艺人茅荣荣,他以7个半小时内连续颠球5万次成为新的吉尼斯纪录创造者,而这个世界纪录至今无人超越.若足球用头顶起,某一次上升高度为80cm,足球的重量为400g,与头顶作用时间△t为0.1s,则足球本次在空中的运动时间;足球给头部的作用力大小.(空气阻力不计,g=10m/s2)( )
如图所示为江西艺人茅荣荣,他以7个半小时内连续颠球5万次成为新的吉尼斯纪录创造者,而这个世界纪录至今无人超越.若足球用头顶起,某一次上升高度为80cm,足球的重量为400g,与头顶作用时间△t为0.1s,则足球本次在空中的运动时间;足球给头部的作用力大小.(空气阻力不计,g=10m/s2)( )| A. | t=0.4s;FN=40N | B. | t=0.4s;FN=68N | C. | t=0.8s;FN=36N | D. | t=0.8s;FN=40N |
16. 如图所示,固定的两圆弧轨道AB和CD长度和高度都相等,滑块和它们之间的动摩擦因数也相同,当滑块分别从AB和CD的顶端自静止起滑到底端时的速度大小为vB和vD,则它们的大小关系为( )
如图所示,固定的两圆弧轨道AB和CD长度和高度都相等,滑块和它们之间的动摩擦因数也相同,当滑块分别从AB和CD的顶端自静止起滑到底端时的速度大小为vB和vD,则它们的大小关系为( )
 如图所示,固定的两圆弧轨道AB和CD长度和高度都相等,滑块和它们之间的动摩擦因数也相同,当滑块分别从AB和CD的顶端自静止起滑到底端时的速度大小为vB和vD,则它们的大小关系为( )
如图所示,固定的两圆弧轨道AB和CD长度和高度都相等,滑块和它们之间的动摩擦因数也相同,当滑块分别从AB和CD的顶端自静止起滑到底端时的速度大小为vB和vD,则它们的大小关系为( )| A. | vB>vD | B. | vB=vD | C. | vB<vD | D. | 无法确定 |
19. 如图,物体A、B静止在光滑水平面上,且mA>mB,现用大小相等的两个力F和F′分别作用在A和B上,使A、B沿一条直线相向运动,然后又先后撤去这两个力,已知这两个力对物体做的功相同,接着两物体碰撞并合为一体.那么AB两物体的合体( )
如图,物体A、B静止在光滑水平面上,且mA>mB,现用大小相等的两个力F和F′分别作用在A和B上,使A、B沿一条直线相向运动,然后又先后撤去这两个力,已知这两个力对物体做的功相同,接着两物体碰撞并合为一体.那么AB两物体的合体( )
 如图,物体A、B静止在光滑水平面上,且mA>mB,现用大小相等的两个力F和F′分别作用在A和B上,使A、B沿一条直线相向运动,然后又先后撤去这两个力,已知这两个力对物体做的功相同,接着两物体碰撞并合为一体.那么AB两物体的合体( )
如图,物体A、B静止在光滑水平面上,且mA>mB,现用大小相等的两个力F和F′分别作用在A和B上,使A、B沿一条直线相向运动,然后又先后撤去这两个力,已知这两个力对物体做的功相同,接着两物体碰撞并合为一体.那么AB两物体的合体( )| A. | 一定停止运动 | B. | 一定向左运动 | ||
| C. | 一定向右运动 | D. | 仍运动,但运动方向不能确定 |
 电学实验补充题
电学实验补充题