题目内容
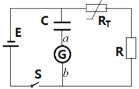
【题目】如图所示,质量为m的物体放在质量为M、倾角为θ的斜面体上,斜面体置于粗糙的水平地面上,用平行于斜面向下的力F拉物体m使其沿斜面向下匀速运动,M始终静止,则下列说法正确的是

A. 地面对M的摩擦力大小为Fcosθ
B. 地面对M的支持力为(M+m)g+Fsinθ
C. 物体m对M的摩擦力的大小为F
D. M对物体m的作用力竖直向上
【答案】AB
【解析】试题分析:物体m沿斜面向下匀速运动,与斜面加速度相同均为零,故可以采用整体法,将物体m与斜面体M看做一个整体,受力分析:
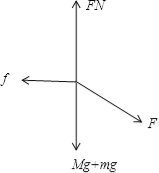

根据平衡条件,水平方向:Fcosθ-f=0,解得f=Fcosθ,所以A正确.竖直方向:FN-(M+m)g-Fsinθ=0,可得FN=(M+m)g+Fsinθ,所以B正确.对物体受力分析如图,物体受到向下的重力mg、拉力F、斜面的作用力(支持力和沿斜面向上的滑动摩擦力),由于物体匀速下滑,根据平衡条件m受到的摩擦力f′=mgsinθ+F,根据牛顿第三定律:物体m对M的摩擦力的大小为mgsinθ+F,故C错误;由受力分析,根据平衡条件:M对物体m的作用力即N与f的合力应该与mg合F的合力等大反向,如图中,可见M对物体m的作用力斜向上,所以D错误.故选AB.

 字词句段篇系列答案
字词句段篇系列答案【题目】某同学利用如下图所示的装置探究功与速度变化的关系:
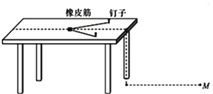
(1)小物块在橡皮筋的作用下弹出,沿水平桌面滑行,之后平抛落至水平地面上,落点即为M1;
(2)在钉子上分别套上2条、3条、4条…同样的橡皮筋,使每次橡皮筋拉伸的长度都保持一致,重复步骤(1),小物块落点分别记为M2、M3、M4…;
(3)测量相关数据,进行数据处理.
①为求出小物块从桌面抛出时的动能,需要测量下列物理量中的 (填正确答案标号,g已知).
A.小物块的质量m |
B.橡皮筋的原长x |
C.橡皮筋的伸长量△x |
D.桌面到地面的高度h |
E.小物块抛出点到落地点的水平距离L
②将几次实验中橡皮筋对小物块做功分别记为W1、W2、W3、…,小物块抛出点到落地点的水平距离分别记为L1、L2、L3、….若功与速度的平方成正比,则应以W为纵坐标, 为横坐标作图,才能得到一条直线.
③由于小物块与桌面之间的摩擦不能忽略,则由此引起的误差属于 (填“偶然误差”或“系统误差”).