题目内容
随着航天技术的发展,在地球周围有很多人造飞行器,其中有一些已超过其设计寿命且能量耗尽.每到太阳活动期,地球的大气层会变厚,这时有些飞行器在大气阻力的作用下,运行的轨道高度将逐渐降低(在其绕地球运动的每一周过程中,轨道高度变化很小均可近似视为匀速圆周运动).为了避免飞行器坠入大气层后对地面设施及人员造成安全威胁,人们设想发射导弹将其在运行轨道上击碎.具体设想是:在导弹的弹头脱离推进装置后,经过一段无动力飞行,从飞行器后下方逐渐接近目标,在进入有效命中距离后引爆弹头并将该飞行器击碎.对于这一过程中的飞行器及弹头,下列说法中正确的是( )
分析:根据匀速圆周运动,万有引力提供向心力公式判断速率和周期的变化,弹头在脱离推进装置之前,在推力作用下做向上的加速运动,处于超重状态.
解答:解:A、根据万有引力提供向心力得:
G
=m
解得:v=
,飞行器轨道高度降低后,它做圆周运动的速率变大,故A正确;
B、根据G
=m
解得:T=
,飞行器轨道高度降低后,它做圆周运动的周期变小,故B错误;
C、弹头在脱离推进装置之前,在推力作用下做向上的加速运动,处于超重状态,故C错误;
D、弹头引爆前瞬间,弹头的半径小于飞行器的半径,根据G
=ma得:a=G
,所以弹头引爆前瞬间,弹头的加速度一定大于此时飞行器的加速度,故D错误.
故选A
G
| Mm |
| R2 |
| v2 |
| R |
解得:v=
|
B、根据G
| Mm |
| R2 |
| 4π2R |
| T2 |
解得:T=
|
C、弹头在脱离推进装置之前,在推力作用下做向上的加速运动,处于超重状态,故C错误;
D、弹头引爆前瞬间,弹头的半径小于飞行器的半径,根据G
| Mm |
| R2 |
| M |
| R2 |
故选A
点评:本题主要考查了万有引力提供向心力公式的直接应用,要比较某个量之间的关系,可以先表示出该物理量,难度适中.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
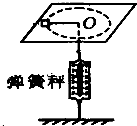 随着航天技术的发展,许多实验可以搬到太空中进行,飞船绕地球做匀速圆周运动时,无法用天平称量物体的质量.假设某宇航员在这种环境下设计了如图所示装置(图中O为光滑的小孔)来间接测量物体的质量:给待测物体一个初速度,使它在桌面上做匀速圆周运动.设飞船中具有基本测量工具..实验时需要测量的物理量是弹簧秤示数F、圆周运动的周期T、
随着航天技术的发展,许多实验可以搬到太空中进行,飞船绕地球做匀速圆周运动时,无法用天平称量物体的质量.假设某宇航员在这种环境下设计了如图所示装置(图中O为光滑的小孔)来间接测量物体的质量:给待测物体一个初速度,使它在桌面上做匀速圆周运动.设飞船中具有基本测量工具..实验时需要测量的物理量是弹簧秤示数F、圆周运动的周期T、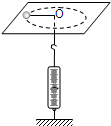 随着航天技术的发展,许多实验可以搬到太空中进行.飞船绕地球做匀速圆周运动时,无法用天平称量物体的质量.假设某宇航员在这种环境下设计了如图所示装置(图中O为光滑的小孔)来间接测量物体的质量:给待测物体一个初速度,使它在桌面上做匀速圆周运动.设飞船中具有基本测量工具.
随着航天技术的发展,许多实验可以搬到太空中进行.飞船绕地球做匀速圆周运动时,无法用天平称量物体的质量.假设某宇航员在这种环境下设计了如图所示装置(图中O为光滑的小孔)来间接测量物体的质量:给待测物体一个初速度,使它在桌面上做匀速圆周运动.设飞船中具有基本测量工具.