题目内容
9.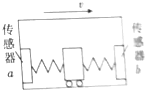 在矩形箱子的前、后壁上各装一个压力传感器,再用两根相同的轻弹簧夹着一个可无摩擦滑动的质量为1.0kg的滑块,两弹簧的另一端分别压在传感器a、b上,其压力大小可直接由传感器读出,如图所示.此装置可以测量汽车的加速度.现将它沿运动方向固定在汽车上,传感器b在前,传感器a在后.已知汽车静止时,传感器a、b的示数均为10N,取g=10m/s2.
在矩形箱子的前、后壁上各装一个压力传感器,再用两根相同的轻弹簧夹着一个可无摩擦滑动的质量为1.0kg的滑块,两弹簧的另一端分别压在传感器a、b上,其压力大小可直接由传感器读出,如图所示.此装置可以测量汽车的加速度.现将它沿运动方向固定在汽车上,传感器b在前,传感器a在后.已知汽车静止时,传感器a、b的示数均为10N,取g=10m/s2.(1)若传感器b的示数为8.0N,求此时汽车的加速度大小和方向.
(2)当汽车以怎样的加速度运动时,传感器b的示数为零?
(3)当汽车以10m/s2的加速度匀减速前进时,求传感器b的示数.
分析 (1)根据胡克定律求出汽车静止时ab弹簧的压缩量,再求出传感器b的示数为8N时,b弹簧恢复的量△x,则a又被压缩了△x,根据胡克定律求解a的示数;
(2)(3)滑块在水平方向上受到的力为a、b两个弹簧施加的弹力,这两个弹力的合力提供加速度,根据牛顿第二定律列式求解
解答 解:(1)由题意知:
Fa0=Fb0=kx0=10N,
Fb=k(x0+△x)=8N
解之得:△Fb=k△x=2N
代入得:Fa=k(x0+△x)=10N+2N=12N
物体受到的合力F=12-8=4N;
对m应用牛顿第二定律得a=$\frac{4}{1}$=4m/s2;
(2)传感器b的示数为零时,△Fb′=10N
则Fa′=Fa0+△Fb′=10N+10N=20N
对m应用牛顿第二定律得Fa′=ma
得a=$\frac{F}{m}$=$\frac{20}{1}$=20m/s2
加速度的方向向左.
(3)当加速度为10m/s2时,合外力为F=ma=1×10=10N;
F=F″a0+△Fb″=10N;
则Fb=10+5=15N;
答:(1)若传感器b的示数为14N,a的示数应该是6N;
(2)当汽车的加速度为20m/s2,方向向左时,传感器b的示数为零;
(3)b的示数为15N;
点评 传感器的示数就是等于该侧弹簧的弹力,也等于弹簧施加给滑块的弹力,对滑块受力分析,运用牛顿第二定律解题.此题要注意弹簧的弹力跟伸长量或缩短量成正比.

练习册系列答案
相关题目
19. 用拉力将一个物体从静止开始拉上一个斜坡.在此过程中,拉力对物体做功为W1,物体克服阻力做的功为W2,物体重力势能的增加量为△EP,动能的增加量为△EK.下列关系式正确的是( )
用拉力将一个物体从静止开始拉上一个斜坡.在此过程中,拉力对物体做功为W1,物体克服阻力做的功为W2,物体重力势能的增加量为△EP,动能的增加量为△EK.下列关系式正确的是( )
 用拉力将一个物体从静止开始拉上一个斜坡.在此过程中,拉力对物体做功为W1,物体克服阻力做的功为W2,物体重力势能的增加量为△EP,动能的增加量为△EK.下列关系式正确的是( )
用拉力将一个物体从静止开始拉上一个斜坡.在此过程中,拉力对物体做功为W1,物体克服阻力做的功为W2,物体重力势能的增加量为△EP,动能的增加量为△EK.下列关系式正确的是( )| A. | W1-W2+△EP=△EK | B. | W1-W2-△EP=△EK | C. | W1+W2+△EP=△EK | D. | W1+W2-△EP=△EK |
4.下列说法中正确的是( )
| A. | 知道水蒸气的摩尔体积和水分子的体积,不能计算出阿伏加德罗常数 | |
| B. | 硬币或钢针能浮于水面上,是由于液体表面张力的作用 | |
| C. | 晶体有固定的熔点,具有规则的几何外形,物理性质具有各向异性 | |
| D. | 影响蒸发快慢以及影响人们对干爽与潮湿感受的因素是空气中水蒸气的压强与同一温度下水的饱和汽压的差距 | |
| E. | 随着科技的发展,将来可以利用高科技手段,将散失在环境中的内能重新收集起来加以利用而不引起其他变化 |
18.手提电脑散热底座一般设置有四个卡位来调节角度,如图甲所示,某同学将电脑放在散热底座上,为了获得更好的舒适度,由原卡位1调至卡位4(如图乙),手提电脑始终处于静止状态,则( )


| A. | 电脑受到的支持力变小 | |
| B. | 电脑受到的摩擦力变大 | |
| C. | 散热底座对电脑作用力的合力不变 | |
| D. | 电脑受到的支持力与摩擦力的大小之和等于其重力 |
