题目内容
如图所示，长为L、质量为2.0kg的长木块A置于光滑水平面上，在A的右端0.50m处有竖直的矮墙（矮于A木块的高度），A与矮墙碰后与墙粘在一起，并保持静止；在A的上表面左端放一质量为1.0kg的铁块B，B的大小不计，B与A的动摩擦因数为0.20。作用在B上的水平向右的拉力F大小为3.2N，在F的作用下A、B都从静止开始运动。求
（1）在A刚碰墙前，A、B运动的加速度分别多大？
（2）若在A刚要碰撞矮墙时，B还在A上面，则此时A、B运动的速度分别多大？
（3）若在A碰撞矮墙时立即撤去拉力F，为使B始终不从A上表面脱落，木块A的长度L至少多长？
（1）在A刚碰墙前，A、B运动的加速度分别多大？
（2）若在A刚要碰撞矮墙时，B还在A上面，则此时A、B运动的速度分别多大？
（3）若在A碰撞矮墙时立即撤去拉力F，为使B始终不从A上表面脱落，木块A的长度L至少多长？
解：（1）假设在F的作用下A、B有相对滑动。则
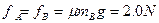
依据牛顿运动定律对B有：
1分
解得：
1分
对A有：
1分
解得：
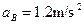1分
由于aA<aB 故以上假设成立
（2）设A从开始运动至碰墙的时间为t.
4分
1分
1分
（3）A碰墙时，B的位移：sB=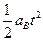
1分
B在A上滑过距离为：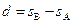
1分
A碰墙后，由牛顿第二定律得：
－μmＢg＝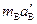
1分
Ｂ经过的位移为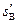
：
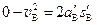1分
木块A的长度L至少为： L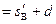
1分
联立解得：
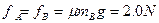
依据牛顿运动定律对B有：
1分解得：
1分对A有：
1分解得：
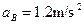1分由于aA<aB 故以上假设成立
（2）设A从开始运动至碰墙的时间为t.
4分 1分 1分（3）A碰墙时，B的位移：sB=
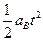1分B在A上滑过距离为：
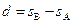1分A碰墙后，由牛顿第二定律得：
－μmＢg＝
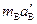1分Ｂ经过的位移为
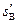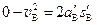： 1分木块A的长度L至少为： L
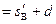1分联立解得：
略
练习册系列答案
相关题目
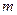的歼10飞机表演后返回某机场，降落在跑道上减速过程简化为两个匀减速直线运动．飞机以速度
着陆后立即打开减速阻力伞，加速度大小为
，运动时间为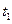
；随后在无阻力伞情况下匀减速直至停下．在平直跑道上减速滑行总路程为
．求：第二个减速阶段飞机运动的加速度大小和时间．
时，下滑的时间为_____；物体到达斜面中点位置的速度为______