题目内容
2. 从地面上以初速度v0=20m/s竖直向上抛出一质量为m=2kg的小球,若运动过程中小球受到的空气阻力与其速率成正比关系,小球运动的速率随时间变化规律如图所示,t1时刻到达最高点,再落回地面,落地时速率为v1=10m/s,且落地前球已经做匀速运动,重力加速度g=10m/s2.求:
从地面上以初速度v0=20m/s竖直向上抛出一质量为m=2kg的小球,若运动过程中小球受到的空气阻力与其速率成正比关系,小球运动的速率随时间变化规律如图所示,t1时刻到达最高点,再落回地面,落地时速率为v1=10m/s,且落地前球已经做匀速运动,重力加速度g=10m/s2.求:(1)小球从抛出到落地过程中克服空气阻力所做的功;
(2)小球抛出瞬间的加速度大小.
分析 (1)运用动能定理可求解球从抛出到落地过程中克服空气阻力所做的功.
(2)落地前匀速运动,则mg-kv1=0.刚抛出时加速度大小为a0,则根据牛顿第二定律mg+kv0=ma0,即可解得球抛出瞬间的加速度大小a0.
解答 解:(1)以小球为研究对象,从地面抛出到落回地面过程中应用动能定理:${W_f}=\frac{1}{2}mv_1^2-\frac{1}{2}mv_0^2$
Wf=-300J
即球从抛出到落地过程中克服空气阻力所做的功Wf=300J
(2)空气阻力:f=kv,下落时速率为v1,且落地前球已经做匀速运动:kv1=mg
$k=\frac{mg}{v_1}=\frac{20}{10}=2Ns/m$
球抛出瞬间:kv0+mg=ma
$a=\frac{{k{v_0}+mg}}{m}=30m/{s^2}$
答:(1)小球从抛出到落地过程中克服空气阻力所做的功为300J;
(2)小球抛出瞬间的加速度大小为30m/s2.
点评 本题考查动能定理的应用,注意掌握应用牛顿定律和动能定理解题的基本方法,注意分析受力及运动过程,从而应用物理规律求解.

练习册系列答案
相关题目
19.如图所示电路中,L为电感线圈,电阻不计,A、B为两灯泡,则( )


| A. | 合上S时,A先亮,B后亮 | |
| B. | 断开S时,A、B同时熄灭 | |
| C. | 断开S时,A立即熄灭,B亮一会儿后熄灭 | |
| D. | 断开S后,B亮一会儿后熄灭,通过B灯电流方向向右 |
13.某同学在做“探究单摆周期与摆长的关系”实验中:

(1)为了减小测量周期的误差,摆球应选经过最低(填“高”或“低”)点的位置时开始计时并计数为0,且用秒表测得经过该位置第n次所用的时间为t,则单摆的周期为$\frac{2t}{n-1}$.
(2)为了寻找单摆周期与摆长的关系,在实验中要改变几次摆长L并测出相应的周期T,从而得出一组对应的T与L的数据,以L为横坐标,T为纵坐标得如图2所示图象.据此你猜测L与T可能有的关系是摆长L与T2(填$\sqrt{T}$、T或T 2)成正比,要证实你的猜测,你应该以摆长L为横坐标,以它(你选定的$\sqrt{T}$、T或T2)为纵坐标作出图象;如果你作出的图象是过O点的直线,那么你的猜测成立.
(3)下表是“探究单摆周期与摆长的关系”实验的有关数据.
①利用上面的数据,在坐标图(图2)中作出L-T 2图象.
②根据图象可知,当地的重力加速度g=9.8m/s2.

(1)为了减小测量周期的误差,摆球应选经过最低(填“高”或“低”)点的位置时开始计时并计数为0,且用秒表测得经过该位置第n次所用的时间为t,则单摆的周期为$\frac{2t}{n-1}$.
(2)为了寻找单摆周期与摆长的关系,在实验中要改变几次摆长L并测出相应的周期T,从而得出一组对应的T与L的数据,以L为横坐标,T为纵坐标得如图2所示图象.据此你猜测L与T可能有的关系是摆长L与T2(填$\sqrt{T}$、T或T 2)成正比,要证实你的猜测,你应该以摆长L为横坐标,以它(你选定的$\sqrt{T}$、T或T2)为纵坐标作出图象;如果你作出的图象是过O点的直线,那么你的猜测成立.
(3)下表是“探究单摆周期与摆长的关系”实验的有关数据.
| 摆长L/m | 0.5100 | 0.6000 | 0.7900 | 1.0000 |
| 周期T2/s2 | 2.0 | 2.4 | 3.2 | 4.0 |
②根据图象可知,当地的重力加速度g=9.8m/s2.
10.下面关于力学现象的解释中正确的是( )
| A. | 小球在空中下落得越来越快,是因为力可以改变物体的运动状态 | |
| B. | 人用力推车车未动,是因为推力小于摩擦力 | |
| C. | 小孩从滑梯上自行下滑,是因为他受到惯性的作用 | |
| D. | 书本静止在课桌上,是因为书本的重力与书本对桌面的压力平衡 |
17.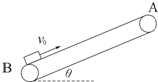 如图所示,传送带AB的倾角为θ,且传送带足够长.现有质量为m可视为质点的物体以v0的初速度从B端开始向上运动,物体与传送带之间的动摩擦因数μ>tanθ,传送带的速度为v(v0<v),方向未知,重力加速度为g.物体在传送带上运动过程中,摩擦力对物体做功的最大瞬时功率是( )
如图所示,传送带AB的倾角为θ,且传送带足够长.现有质量为m可视为质点的物体以v0的初速度从B端开始向上运动,物体与传送带之间的动摩擦因数μ>tanθ,传送带的速度为v(v0<v),方向未知,重力加速度为g.物体在传送带上运动过程中,摩擦力对物体做功的最大瞬时功率是( )
 如图所示,传送带AB的倾角为θ,且传送带足够长.现有质量为m可视为质点的物体以v0的初速度从B端开始向上运动,物体与传送带之间的动摩擦因数μ>tanθ,传送带的速度为v(v0<v),方向未知,重力加速度为g.物体在传送带上运动过程中,摩擦力对物体做功的最大瞬时功率是( )
如图所示,传送带AB的倾角为θ,且传送带足够长.现有质量为m可视为质点的物体以v0的初速度从B端开始向上运动,物体与传送带之间的动摩擦因数μ>tanθ,传送带的速度为v(v0<v),方向未知,重力加速度为g.物体在传送带上运动过程中,摩擦力对物体做功的最大瞬时功率是( )| A. | μmg$\sqrt{{v^2}+v_0^2}$cosθ | B. | μmgv0cosθ | ||
| C. | μmgvcosθ | D. | $\frac{1}{2}$μmg(v+v0)cosθ |
7. 如图所示,水平面上固定光滑的等腰直角三角形支架OAB,质量m的小环甲套在OA上,质量m的小环乙套在OB边上接近O点处,两环之间用长为L的轻绳连接. 两环整体的重心在绳子中点处,若将两小环从图示位置静止释放,下列说法中正确的是( )
如图所示,水平面上固定光滑的等腰直角三角形支架OAB,质量m的小环甲套在OA上,质量m的小环乙套在OB边上接近O点处,两环之间用长为L的轻绳连接. 两环整体的重心在绳子中点处,若将两小环从图示位置静止释放,下列说法中正确的是( )
 如图所示,水平面上固定光滑的等腰直角三角形支架OAB,质量m的小环甲套在OA上,质量m的小环乙套在OB边上接近O点处,两环之间用长为L的轻绳连接. 两环整体的重心在绳子中点处,若将两小环从图示位置静止释放,下列说法中正确的是( )
如图所示,水平面上固定光滑的等腰直角三角形支架OAB,质量m的小环甲套在OA上,质量m的小环乙套在OB边上接近O点处,两环之间用长为L的轻绳连接. 两环整体的重心在绳子中点处,若将两小环从图示位置静止释放,下列说法中正确的是( )| A. | 两环整体重心的运动轨迹是以O为圆心,以R=$\frac{L}{2}$为半径的$\frac{1}{4}$圆弧 | |
| B. | 两环总动能达到最大时,两环的速度大小都是v=$\sqrt{\frac{2-\sqrt{2}}{2}gL}$ | |
| C. | 小环甲向上运动过程中,绳子拉力对小环甲一直做正功 | |
| D. | 小环乙向下运动过程中,小环乙重力的功率一直增大 |
 在用打点计时器验证机械能守恒定律的实验中,质量m=1.00kg的重物自由下落,打点计时器在纸带上打出一系列点.如图所示为选取的一条符合实验要求的纸带,O为第一个点,A、B、C为从合适位置开始选取的三个连续点(其他点未画出).已知打点计时器每隔0.02s打一次点,当地的重力加速度g=9.80m/1,.那么:
在用打点计时器验证机械能守恒定律的实验中,质量m=1.00kg的重物自由下落,打点计时器在纸带上打出一系列点.如图所示为选取的一条符合实验要求的纸带,O为第一个点,A、B、C为从合适位置开始选取的三个连续点(其他点未画出).已知打点计时器每隔0.02s打一次点,当地的重力加速度g=9.80m/1,.那么: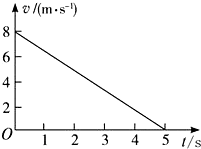 如图为质点运动的v-t图象,由图可知该质点运动的初速度为8m/s,2s末的速度为4.8m/s.
如图为质点运动的v-t图象,由图可知该质点运动的初速度为8m/s,2s末的速度为4.8m/s.