题目内容
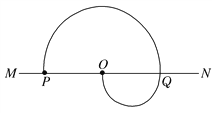
【题目】如图所示,AB为水平轨道,A、B间距离s=1.25m,BCD是半径为R=0.40m的竖直半圆形轨道,B为两轨道的连接点,D为轨道的最高点.有一小物块质量为m=1.0kg,小物块在F=10N的水平力作用下从A点由静止开始运动,到达B点时撤去力F,它与水平轨道和半圆形轨道间的摩擦均不计.g取10m/s2,求:

(1)撤去力F时小物块的速度大小;
(2)小物块通过D点瞬间对轨道的压力大小;
(3)小物块通过D点后,再一次落回到水平轨道AB上,落点和B点之间的距离大小.
【答案】(1)5m/s(2)12.5N(3)1.2m
【解析】
(1)小物体在AB段做匀加速直线运动,水平方向受拉力由动能定理求解撤去力F时小物块的速度大小;
(2)小物块从B到D点过程,只有重力做功,根据动能定理求得物块通过D点瞬间的速度大小,由牛顿第二定律和第三定律求解对轨道的压力大小;
(3)物块通过D点后做平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动,由运动学公式求解落点和B点之间的距离大小.
(1)当物块从A滑向B时,设在B点撤去F时速度大小为vB.
根据动能定理得:Fs=![]()
得 vB=5m/s
(2)小物块从B到D点瞬间,由动能定理得:-mg2R=![]()
解得:vD=3m/s
根据牛顿第二定律得:FD+mg=m![]()
解得:FD=12.5N
由牛顿第三定律知压力大小为FD′=FD=12.5N
(3)物块通过D点后做平抛运动,有:
2R=![]() gt2
gt2
x=vDt
解得:x=1.2m

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目