Question

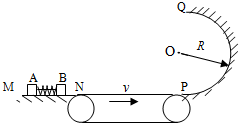如图所示，光滑的水平导轨MN右端N处与水平传送带平滑连接，传送带长度L=0.8m，以恒定速率v=3.0m/s向右匀速运动．传送带的右端P处平滑连接着在竖直平面内、半径为R=0.4m的光滑半圆轨道PQ．质量均为m=0.2kg A、B两滑块用细绳相连，其间有一压缩轻弹簧，开始时它们以V₀=1m/s的速度在水平导轨MN上向右匀速运动．现使细绳断开，弹簧伸展，滑块B脱离弹簧后滑上传送带，从传送带右端滑出并沿半圆轨道运动到最高点Q后水平飞出，又正好落回N点．已知滑块B与传送带之间的动摩擦因数μ=

5

16

，取g=10m/s²．求：
（1）滑块B到达Q点时速度的大小；
（2）滑块B在半圆轨道P处对轨道的压力；
（3）压缩的轻弹簧的弹性势能E_p．

Answer 1

分析：（1）据题意，滑块B从Q处飞出后做平抛运动，根据平抛运动的规律，由高度2R和水平位移L求解滑块B到达Q点时速度的大小；
（2）滑块B从P运动到Q过程中，只有重力做功，机械能守恒，即可求出它经过B点的速度，在P点由重力和支持力的合力提供其向心力，根据牛顿运动定律求解滑块B在半圆轨道P处对轨道的压力；
（3）根据滑块B到达P点的速度与传送带速度的关系，分析滑块B在传送带上的运动情况，由牛顿牛顿第二定律和运动学公式求出滑块B在弹簧伸展后的速度．细绳断开，弹簧伸展的过程，B、A、弹簧系统动量守恒和机械能守恒，即可求解压缩的轻弹簧的弹性势能E_p．

解答：解：（1）．滑块B从Q飞出后做平抛运动，有：

1

2

(2m)

v

2 0

    L=v_Qt …（1）
   2R=

1

2

gt2 …（2）
由（1）（2）解得 v_Q=2m/s．
（2）．滑块B从P运动到Q过程中满足机械能守恒，有：
  

1

2

m

v

2 Q

+2mgR=

1

2

m

v

2 P

…（3）
在P点有：N-mg=

m v 2 P

R

…（4）
由（3）（4）解得：N=12N
根据牛顿第三定律得：滑块B在半圆轨道P处对轨道的压力N′=N=12N，方向竖直向下；
 3．由（3）得：vP=

v 2 Q +4gR

=2

5

m/s，故可知滑块B在皮带上做匀减速运动，加速度：
a=-

f

m

=-μg …（5）
又

v

2 P

-

v

2 N

=2aL …（6）
细绳断开后弹簧伸展过程，A、B组成的系统动量守恒：2mv₀=mv_N+mv_A …（7）
轻弹簧与A、B组成的系统能量守恒：Ep+

1

2

(2m)

v

2 0

=

1

2

m

v

2 N

+

1

2

m

v

2 A

…（8）
由（5）（6）（7）（8）解得：弹簧的弹性势能：Ep=3.4J
答：
（1）滑块B到达Q点时速度的大小是2m/s；
（2）滑块B在半圆轨道P处对轨道的压力是12N；
（3）压缩的轻弹簧的弹性势能E_p是3.4J．

点评：本题综合了牛顿运动定律、平抛运动、机械能守恒定律、动量守恒定律等多方面的知识，分析过程，把握解题规律是关键．难度适中．