题目内容
17.如图所示,在水平轨道右侧安放半径为R的竖直圆槽形光滑轨道,水平轨道的PQ段铺设特殊材料,调节其初始长度为l;水平轨道左侧有一轻质弹簧左端固定,弹簧处于自然伸长状态.小物块A静止放置在弹簧右端,A与弹簧接触但不拴接;小物块B从轨道右侧以初速度v0冲上轨道,通过圆形轨道、水平轨道后与物块A发生对心碰撞且瞬间粘连,之后A、B一起压缩弹簧并被弹簧以原速率弹回,经水平轨道返回圆形轨道.物块A、B均可视为质点.已知R=0.2m,l=1.0m,v0=6m/s,物块A、B质量均为m=1kg,与PQ段间的动摩擦因数均为μ=0.2,轨道其他部分摩擦不计.取g=10m/s2.求:
(1)物块B与物块A碰撞前速度大小;
(2)物块B与物块A碰后返回到圆形轨道的高度;
(3)调节PQ段的长度l,B仍以v0从轨道右侧冲上轨道,当l满足什么条件时,A、B物块能返回圆形轨道且能沿轨道运动而不会脱离轨道?

分析 (1)物块A从Q到P过程中,运用动能定理,结合摩擦力做功,从而求出物块A与弹簧刚接触时的速度大小.
(2)根据运动学公式求得回到圆轨道的速度大小,再根据动能定理求出A能够上升的高度,并讨论能否达到此高度.
(3)A物块能返回圆形轨道且能沿轨道运动而不会脱离轨道,要么能够越过圆轨道的最高点,要么在圆轨道中上升的高度不要超过圆轨道的半径,结合动能定理、动量守恒定律和牛顿第二定律求出l所满足的条件.
解答 解:(1)物块A冲上圆形轨道后回到最低点速度为v0=$2\sqrt{3}$m/s,
与弹簧接触瞬间,$-μmgl=\frac{1}{2}mv_1^2-\frac{1}{2}mv_0^2$,
可得,物块A与弹簧刚接触时的速度大小${v_1}=2\sqrt{2}$m/s;
(2)A被弹簧以原速率v1弹回,向右经过PQ段,
有$v_2^2-v_1^2=-2μgl$;解得A速度 v2=2m/s,
A滑上圆形轨道,有$-mgh=0-\frac{1}{2}mv_2^2$,
(也可以应用 $-μ×mgl-mgh=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2$)
可得,返回到右边轨道的高度为h=0.2m=R,符合实际.
(3)物块A以v0冲上轨道直到回到PQ段右侧,
有$v'_1^2-v_0^2=-2μg×2l$,
可得,A回到右侧速度:$v'_1^2=(12-8l){(m/s)^2}$,
要使A能返回右侧轨道且能沿轨道运动而不脱离轨道,则有:
①若A沿轨道上滑至最大高度h时,速度减为0,则h满足:0<h≤R,
根据机械能守恒:$\frac{1}{2}mv'_1^2=mgh$联立可得,1.0m≤l<1.5m;
②若A能沿轨道上滑至最高点,则满足:$\frac{1}{2}mv'_1^2=mg×2R+\frac{1}{2}mv'_2^2$且$m\frac{v'_2^2}{R}≥mg$,
联立得 l≤0.25m,综上所述,要使A物块能第一次返回圆形轨道并沿轨道运动而不脱离轨道,
l满足的条件是1.0m≤l<1.5m或 l≤0.25m;
答:(1)物块A与弹簧刚接触时的速度大小为2$\sqrt{2}$m/s.
(2)物块A被弹簧以原速率弹回返回到圆形轨道的高度0.2m.
(3)A物块能第一次返回圆形轨道且能沿轨道运动而不会脱离轨道的条件是:1.0m≤l<1.5m或 l≤0.25m.
点评 本题综合考查了动量守恒定律、动能定理、牛顿第二定律,以及知道小球不脱离圆轨道的条件,综合性较强,对学生的能力要求较高,需加强训练.

 如图所示,在倾角为θ=30°的光滑斜面上,物块A、B质量分别为m和2m.物块A静止在轻弹簧上面,物块B用细线与斜面顶端相连,A、B紧挨在一起但A、B之间无弹力,已知重力加速度为g.某时刻将细线剪断,则细线剪断瞬间,下列说法错误的是( )
如图所示,在倾角为θ=30°的光滑斜面上,物块A、B质量分别为m和2m.物块A静止在轻弹簧上面,物块B用细线与斜面顶端相连,A、B紧挨在一起但A、B之间无弹力,已知重力加速度为g.某时刻将细线剪断,则细线剪断瞬间,下列说法错误的是( )| A. | 物块B的加速度为$\frac{g}{2}$ | B. | 物块A.B间的弹力为$\frac{mg}{2}$ | ||
| C. | 弹簧的弹力为$\frac{mg}{3}$ | D. | 物块A的加速度为$\frac{g}{3}$ |
| A. | 8 m | B. | 9 m | C. | 10 m | D. | 11 m |
 质点所受的合力F随时间变化的规律如图所示,力的方向始终在一直线上.已知t=0时质点的速度为零.在图示t1、t2、t3和t4各时刻关于其动能的大小说法正确的是( )
质点所受的合力F随时间变化的规律如图所示,力的方向始终在一直线上.已知t=0时质点的速度为零.在图示t1、t2、t3和t4各时刻关于其动能的大小说法正确的是( )| A. | t1时刻动能最大 | B. | t2时刻动能最大 | ||
| C. | t2时刻动能为零 | D. | t1和t3时刻动能相等 |
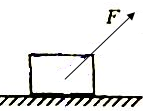 如图所示,粗糙水平面上有一质量为m的物体,受到一个斜向上的外力F的作用.判断正确的是( )
如图所示,粗糙水平面上有一质量为m的物体,受到一个斜向上的外力F的作用.判断正确的是( )| A. | 物体静止时可能受到3个力的作用 | |
| B. | 物体静止时一定受到4个力的作用 | |
| C. | 物体在水平面上运动时可能受到2个力的作用 | |
| D. | 物体在水平面上匀速运动时存在F的最小值 |
 如图,质量为M的小船在静止水面上以速率V0 向右匀速行驶,一质量为m的救生员站在船尾,相对小船静止.若救生员以相对水面速率v水平向左跃入水中,则救生员跃出后小船的速率为v0+$\frac{m}{M}$(v0+v).
如图,质量为M的小船在静止水面上以速率V0 向右匀速行驶,一质量为m的救生员站在船尾,相对小船静止.若救生员以相对水面速率v水平向左跃入水中,则救生员跃出后小船的速率为v0+$\frac{m}{M}$(v0+v).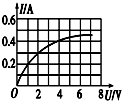 如图所示为一个小灯泡的电流与它两端电压的变化关系曲线.若把三个这样的灯泡串联后,接到电压恒定的3V电源上,求流过小灯泡的电流为0.2A,小灯泡的电阻为5Ω.
如图所示为一个小灯泡的电流与它两端电压的变化关系曲线.若把三个这样的灯泡串联后,接到电压恒定的3V电源上,求流过小灯泡的电流为0.2A,小灯泡的电阻为5Ω.