题目内容
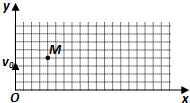 在如图所示的xoy平面内(y轴的正方向竖直向上)存在着水平向右的匀强电场,有带正电的小球自坐标原点O沿y轴的正方向竖直向上抛出,它的初动能为5J,不计空气阻力,当它上升到最高点M时,动能为4J.
在如图所示的xoy平面内(y轴的正方向竖直向上)存在着水平向右的匀强电场,有带正电的小球自坐标原点O沿y轴的正方向竖直向上抛出,它的初动能为5J,不计空气阻力,当它上升到最高点M时,动能为4J.(1)试分析说明带电小球被抛出后沿竖直方向和水平方向分别做什么运动;
(2)若带电小球落回到x轴上的P点,在图中标出P点的位置,并大致绘出其轨迹;
(3)求带电小球到达P点的动能.
分析:(1)对小球进行受力分析可知,小球受到重力(竖直向下)和电场力(水平向右)的作用;由于小球初速度竖直向上,初速度水平分量为零,故小球竖直方向做匀减速直线运动(竖直上抛运动),水平方向做初速度为零的匀加速直线运动;
(2)由竖直上抛运动的特点分析运动的时间关系,从而求出运动的位移之比,进而画出图象;
(3)根据运动分解可知,竖直方向竖直上抛,水平方向做初速度为零的匀加速直线运动,结合分运动的等时性,运用运动学公式,即可求解.
(2)由竖直上抛运动的特点分析运动的时间关系,从而求出运动的位移之比,进而画出图象;
(3)根据运动分解可知,竖直方向竖直上抛,水平方向做初速度为零的匀加速直线运动,结合分运动的等时性,运用运动学公式,即可求解.
解答: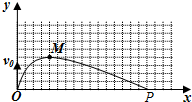 解:(1)对小球进行受力分析可知,小球受到重力(竖直向下)和电场力(水平向右)的作用;
解:(1)对小球进行受力分析可知,小球受到重力(竖直向下)和电场力(水平向右)的作用;
由于小球初速度竖直向上,初速度水平分量为零,故小球竖直方向做匀减速直线运动(竖直上抛运动),水平方向做初速度为零的匀加速直线运动.
(2)由竖直上抛运动的特点可知,小球从O点到M的时间与从M点到P点的时间相等,又水平方向做初速度为零的匀加速直线运动,故两端连续相等的时间间隔内水平位移之比为1:3,得P点坐标如图所示;
(3)设小球在M点的速度为v1,在P点的速度为v,将v沿水平方向和竖直方向分解,水平分量为v2,竖直分量为v3;
根据竖直上抛运动的特点知:v3=v0----------①
水平方向做匀加速直线运动,v1沿水平方向,故v2=2v1----------②
由题意可知Eko=
m
=5J,EkM=
m
=4J----------③
P点的动能Ekp=
mv2=
m(
+
)----------④
由①②③④四式,解得EkP=21J.
答:(1)小球竖直方向做匀减速直线运动(竖直上抛运动),水平方向做初速度为零的匀加速直线运动;
(2)如图所示;
(3)带电小球到达P点的动能为21J.
 解:(1)对小球进行受力分析可知,小球受到重力(竖直向下)和电场力(水平向右)的作用;
解:(1)对小球进行受力分析可知,小球受到重力(竖直向下)和电场力(水平向右)的作用;由于小球初速度竖直向上,初速度水平分量为零,故小球竖直方向做匀减速直线运动(竖直上抛运动),水平方向做初速度为零的匀加速直线运动.
(2)由竖直上抛运动的特点可知,小球从O点到M的时间与从M点到P点的时间相等,又水平方向做初速度为零的匀加速直线运动,故两端连续相等的时间间隔内水平位移之比为1:3,得P点坐标如图所示;
(3)设小球在M点的速度为v1,在P点的速度为v,将v沿水平方向和竖直方向分解,水平分量为v2,竖直分量为v3;
根据竖直上抛运动的特点知:v3=v0----------①
水平方向做匀加速直线运动,v1沿水平方向,故v2=2v1----------②
由题意可知Eko=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
P点的动能Ekp=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 2 |
| v | 2 3 |
由①②③④四式,解得EkP=21J.
答:(1)小球竖直方向做匀减速直线运动(竖直上抛运动),水平方向做初速度为零的匀加速直线运动;
(2)如图所示;
(3)带电小球到达P点的动能为21J.
点评:解答本题时要注意以下三点:小球竖直方向做竖直上抛运动,水平方向做匀加速运动;M点为最高点,则竖直方向的分速度为零;竖直方向的运动具有对称性.注意不一定求动能就把速度求出来,有时只需要知道速度之比即可,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 (2011?浙江模拟)如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.40T,方向垂直纸面向里,电场强度E=2.0×105V/m,PQ为板间中线.紧靠平行板右侧边缘xOy坐标系的第一象限内,有垂直纸面的正三角形匀强磁场区域,磁感应强度B2=0.25T.一束带电量q=8.0×10-19C,质量m=8.0×10-26 kg的正离子从P点射入平行板间,不计重力,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射向三角形磁场区,离子通过x轴时的速度方向与x轴正方向夹角为60°.则:
(2011?浙江模拟)如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.40T,方向垂直纸面向里,电场强度E=2.0×105V/m,PQ为板间中线.紧靠平行板右侧边缘xOy坐标系的第一象限内,有垂直纸面的正三角形匀强磁场区域,磁感应强度B2=0.25T.一束带电量q=8.0×10-19C,质量m=8.0×10-26 kg的正离子从P点射入平行板间,不计重力,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射向三角形磁场区,离子通过x轴时的速度方向与x轴正方向夹角为60°.则: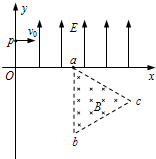 (2013?安徽)如图所示的平面直角坐标系xOy,在第Ⅰ象限内有平行于y轴的匀强电场,方向沿y正方向;在第Ⅳ象限的正三角形abc区域内有匀强磁场,方向垂直于xOy平面向里,正三角形边长为L,且ab边与y轴平行.一质量为m、电荷量为q的粒子,从y轴上的p(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限,又经过磁场从y轴上的某点进入第Ⅲ象限,且速度与y轴负方向成45°角,不计粒子所受的重力.求:
(2013?安徽)如图所示的平面直角坐标系xOy,在第Ⅰ象限内有平行于y轴的匀强电场,方向沿y正方向;在第Ⅳ象限的正三角形abc区域内有匀强磁场,方向垂直于xOy平面向里,正三角形边长为L,且ab边与y轴平行.一质量为m、电荷量为q的粒子,从y轴上的p(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限,又经过磁场从y轴上的某点进入第Ⅲ象限,且速度与y轴负方向成45°角,不计粒子所受的重力.求: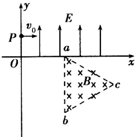 如图所示的平面直角坐标系xOy,在第Ⅰ象限内有平行于y轴的匀强电场,方向沿y轴正方向;在第Ⅳ象限的正三角形abc区域内有匀强磁场,方向垂直于xOy平面向里,正三角形边长为L,且ab边与y轴平行.一质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限,又经过磁场从y轴上的某点进入第Ⅲ象限,且速度与y轴负方向成45°角,不计粒子所受的重力.求:
如图所示的平面直角坐标系xOy,在第Ⅰ象限内有平行于y轴的匀强电场,方向沿y轴正方向;在第Ⅳ象限的正三角形abc区域内有匀强磁场,方向垂直于xOy平面向里,正三角形边长为L,且ab边与y轴平行.一质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限,又经过磁场从y轴上的某点进入第Ⅲ象限,且速度与y轴负方向成45°角,不计粒子所受的重力.求: