题目内容
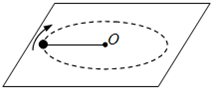 如图,绳子的一端固定在O点,另一端拴一重物在水平面上做匀速圆周运动,下列表述正确的是( )
如图,绳子的一端固定在O点,另一端拴一重物在水平面上做匀速圆周运动,下列表述正确的是( )分析:重物在水平面上做匀速圆周运动时,绳子的拉力提供向心力,根据牛顿第二定律,向心力分别用周期、角速度、线速度表示,研究拉力与它们的关系,分析求解.
解答:解:A、圆周运动速度方向是切线方向,时刻改变,一定有加速度,合力一定不为零,故A错误;
B、根据牛顿第二定律得:F=m
,m一定,当周期T相同时,绳长r越长,绳子拉力F越大,绳子越容易断,故B错误;
C、根据牛顿第二定律得:F=mω2r,m一定,当ω相同时,绳长r越长,绳子拉力F越大,绳子越容易断,故C正确;
D、根据牛顿第二定律得:F=
,m一定,当v相同时,绳长r越长,绳子拉力F越小,绳子越不容易断,故D错误;
故选C.
B、根据牛顿第二定律得:F=m
| 4π2r |
| T2 |
C、根据牛顿第二定律得:F=mω2r,m一定,当ω相同时,绳长r越长,绳子拉力F越大,绳子越容易断,故C正确;
D、根据牛顿第二定律得:F=
| v2 |
| r |
故选C.
点评:本题考查灵活选择公式的能力,向心力的公式形式通常有下列几种,在不同条件下选用不同的形式:
Fn=m(2πn)2r=m
=m
=mω2r=mvω.
Fn=m(2πn)2r=m
| v2 |
| r |
| 4π2r |
| T2 |

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 (2007?广州模拟)如图所示,绳子的一端固定在O点,另一端拴一重物在水平面上做匀速圆周运动( )
(2007?广州模拟)如图所示,绳子的一端固定在O点,另一端拴一重物在水平面上做匀速圆周运动( )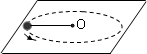
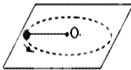
 如图,绳子的一端固定在O点,另一端拴一重物在水平面上做匀速圆周运动,下列表述正确的是( )
如图,绳子的一端固定在O点,另一端拴一重物在水平面上做匀速圆周运动,下列表述正确的是( )