题目内容
 两个小球1和2的质量分别是m1=2.0kg,m2=1.6kg,球1静止于光滑的水平面上的A点,球2在水平面上从远处沿两球心连线向着1球运动.假设两球相距L≤18m时存在着恒定的斥力F,L>18m时无相互作用力.当两球相距最近时,它们的距离为d=2.0m,球2的速度为v=4m/s.求:
两个小球1和2的质量分别是m1=2.0kg,m2=1.6kg,球1静止于光滑的水平面上的A点,球2在水平面上从远处沿两球心连线向着1球运动.假设两球相距L≤18m时存在着恒定的斥力F,L>18m时无相互作用力.当两球相距最近时,它们的距离为d=2.0m,球2的速度为v=4m/s.求:(1)两球间的斥力的大小.
(2)球1速度达最大时距A点的最小距离S.
分析:(1)当两球速度相等时,两球相距最近,根据动量守恒定律列出等式,
在两球相距L>18m时无相互作用力,B球做匀速直线运动,两球相距L≤18m时存在着恒定斥力F,B球做匀减速运动,由动能定理可得相互作用力
(2)球1速度达到最大时二者间距恢复为L.根据动量守恒定律和动能定理列出等式求解.
在两球相距L>18m时无相互作用力,B球做匀速直线运动,两球相距L≤18m时存在着恒定斥力F,B球做匀减速运动,由动能定理可得相互作用力
(2)球1速度达到最大时二者间距恢复为L.根据动量守恒定律和动能定理列出等式求解.
解答:解:(1)设最近时速度均为V,1、2两球发生的位移分别为S1、S2,由动量守恒定律得:
m2v0=(m1+m2)v
对2球由动能定理得:
FS2=
m2
-
m2v2
FS1=
m2V2
几何关系得:S1+L=S2+d
联立以上等式得:V0=9m/s F=2.25N
(2)设球1达最大速度为V1,这时球2速度为V2,球1、2的位移分别为S′1、S′2,球1速度达到最大时二者间距恢复为L,
由动量守恒得:m2V0=m1V1+m2V2
由动能定理有:
FS′1=
m1
FS′2=
m2
-
m2
几何关系得:S1′=S2′
联立以上四式得:S1′=28.4m V1=8.0m/s
答:(1)两球间的斥力的大小是2.25N.
(2)球1速度达最大时距A点的最小距离是28.4m.
m2v0=(m1+m2)v
对2球由动能定理得:
FS2=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
FS1=
| 1 |
| 2 |
几何关系得:S1+L=S2+d
联立以上等式得:V0=9m/s F=2.25N
(2)设球1达最大速度为V1,这时球2速度为V2,球1、2的位移分别为S′1、S′2,球1速度达到最大时二者间距恢复为L,
由动量守恒得:m2V0=m1V1+m2V2
由动能定理有:
FS′1=
| 1 |
| 2 |
| v | 2 1 |
FS′2=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 2 |
几何关系得:S1′=S2′
联立以上四式得:S1′=28.4m V1=8.0m/s
答:(1)两球间的斥力的大小是2.25N.
(2)球1速度达最大时距A点的最小距离是28.4m.
点评:本题综合考查了动量守恒定律和动能定理,综合性较强.知道速度相等时,两球相距最近,以及知道恒力与与相对位移的乘积等于系统动能的损失是解决本题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
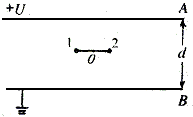 如图所示,水平放置的平行金属板的B板接地,A、B两板间的电势差为+U,两板间为匀强电场,间距为d.在两板之间有一长为l的绝缘轻杆,且l<d,可绕其中点O在竖直面内无摩擦地转动,杆的两端分别连着两个小球1和2,它们的质量分别为m1和m2,且m1<m2,它们的电荷量大小分别为q1和q2,小球1带负电,小球2带正电.设两球运动过程中极板上的电荷分布情况不变.当杆由图示水平位置从静止开始转到竖直位置时两球的总动能为( )
如图所示,水平放置的平行金属板的B板接地,A、B两板间的电势差为+U,两板间为匀强电场,间距为d.在两板之间有一长为l的绝缘轻杆,且l<d,可绕其中点O在竖直面内无摩擦地转动,杆的两端分别连着两个小球1和2,它们的质量分别为m1和m2,且m1<m2,它们的电荷量大小分别为q1和q2,小球1带负电,小球2带正电.设两球运动过程中极板上的电荷分布情况不变.当杆由图示水平位置从静止开始转到竖直位置时两球的总动能为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
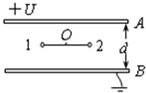 如图所示,水平放置的金属平行板的B板接地,A板电势为+U,两板间距离为d,d比两板的尺寸小很多,在两板之间有一长为l的绝缘轻杆,可绕固定轴O(O居球1、2连线中点)在竖直面内无摩擦地自由转动,杆的两端分别连着两个小球1和2,它们的质量分别为m1和m2,m1<m2,它们的带电量分别为-q1和+q2,q1<q2,当杆由图示水平位置从静止开始转到竖直位置时( )
如图所示,水平放置的金属平行板的B板接地,A板电势为+U,两板间距离为d,d比两板的尺寸小很多,在两板之间有一长为l的绝缘轻杆,可绕固定轴O(O居球1、2连线中点)在竖直面内无摩擦地自由转动,杆的两端分别连着两个小球1和2,它们的质量分别为m1和m2,m1<m2,它们的带电量分别为-q1和+q2,q1<q2,当杆由图示水平位置从静止开始转到竖直位置时( )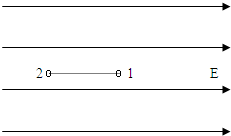 (2004?广东)在场强为E的匀强电场中固定放置两个小球1和2,它们的质量相等,电荷分别为q1和q2(q1≠q2).球1和球2的连线平行于电场线,如图.现同时放开1球和2球,于是它们开始在电场力的作用下运动,如果球1和球2之间的距离可以取任意有限值,则两球刚被放开时,它们的加速度可能是( )
(2004?广东)在场强为E的匀强电场中固定放置两个小球1和2,它们的质量相等,电荷分别为q1和q2(q1≠q2).球1和球2的连线平行于电场线,如图.现同时放开1球和2球,于是它们开始在电场力的作用下运动,如果球1和球2之间的距离可以取任意有限值,则两球刚被放开时,它们的加速度可能是( )