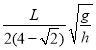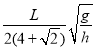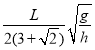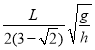题目内容
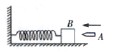
【题目】质量为M的小车，以速度
在光滑水平地面上前进，车上站着一个质量为m的人问：当人以对车的速度
向后水平跳出后，车的速度为多大？
【答案】
【解析】
错解 错解一：设人跳出瞬间车速为v，则此时车的动量为M，根据动量守恒定律有
解得
.
错解二：设人跳出后车速为U，此时车的动量为Mv，人的动量为
，根据动量守恒定律有
解得
.
错解三：设车的前进方向为正方向，人在跳出车后，车的动量为Mv，人的动量为
，根据动量守恒定律有
解得
.
错解四：设车前进方向为正方向，则人跳出车后，车的动量为Mv，人的动量为
，根据动量守恒定律有
解得
.
错因分析 错解一错因：动量守恒的对象应为车和人组成的系统，而错解一中把人跳离车后的动量丢掉了，即以系统的一部分（车）来代替了系统（车和人）.
错解二错因：没有考虑到人跳离车前后动量方向的变化，而是简单地采用了代数运算，即忽略了动量的矢量性.
错解三错因：参考系发生了变化人跳离前人与车的动量是相对地的，人跳离车后车的动量（Mv）也是相对地的，而人跳离车后人的动量（）却是相对于车而言的，所以错解三错误.
错解四错因：对速度瞬时性的分析出错.
是人未跳离车之前系统
的速度，不能代表人跳离车后瞬间人的动量.
正解
解析： 选地面为参考系，以小车前进的方向为正方向，则人跳出车后，人的动量为
，根据动量守恒定律有
解得
.
练习册系列答案
相关题目
