题目内容
16. 如图所示,一倾斜放置的传送带与水平面的倾角θ=37°,在电动机的带动下以v=2m/s的速率顺时针方向匀速运行,M、N为传送带的两个端点,MN两点间的距离L=7m,N端有一离传送带很近的挡板P可将传送带上的物块挡住,在传送带上的O处由静止释放一质量为1kg的可视为质点的木块,木块与传送带间的动摩擦因数μ=0.5.木块由静止释放后沿传送带向下运动,并与挡板P发生碰撞,已知碰撞时间极短,木块B与挡板P碰撞前后速度大小不变,OM间距离L=3m,sin37°=0.6,cos37°=0.8,g取10m/s2,传送带与轮子间无相对滑动,不计轮轴处的摩擦.
如图所示,一倾斜放置的传送带与水平面的倾角θ=37°,在电动机的带动下以v=2m/s的速率顺时针方向匀速运行,M、N为传送带的两个端点,MN两点间的距离L=7m,N端有一离传送带很近的挡板P可将传送带上的物块挡住,在传送带上的O处由静止释放一质量为1kg的可视为质点的木块,木块与传送带间的动摩擦因数μ=0.5.木块由静止释放后沿传送带向下运动,并与挡板P发生碰撞,已知碰撞时间极短,木块B与挡板P碰撞前后速度大小不变,OM间距离L=3m,sin37°=0.6,cos37°=0.8,g取10m/s2,传送带与轮子间无相对滑动,不计轮轴处的摩擦.(1)求木块与挡板P第一次碰撞后所达到的最高位置与挡板P的距离.
(2)经过足够长时间后,电动机的输出功率保持不变,求此输出功率大小.
分析 (1)根据牛顿第二定律求出木块下滑的加速度,从而结合速度位移公式求出与挡板碰撞的速度,反弹后,速度大于传送带速度,摩擦力向下,速度与传送带速度相等后,摩擦力向上,根据牛第二定律分别求出上滑过程中的加速度,结合运动学公式求出木块B所达到的最高位置与挡板P的距离.
(2)经过多次碰撞后木块B以2m/s的速度被反弹,最终在距N点1m的范围内不断以加速度a2做向上的减速运动和向下的加速运动.木块B对传送带有一与传送带运动方向相反的阻力,结合P=μmgvcosθ求出电动机的输出功率.
解答 解:(1)由静止释放后,木块B沿传送带向下做匀加速运动,其加速度为a1,运动距离LON=4m,第一次与P碰撞前的速度为v1
a1=gsinθ-μgcosθ=2m/s2,v1=$\sqrt{2{a}_{1}{L}_{ON}}$=4m/s,
与挡板P第一次碰撞后,木块B以速度v1被反弹,先沿传送带向上以加速度a2做匀减速运动直到速度为v,此过程运动距离为s1;之后以加速度a1继续做匀减速运动直到速度为0,此时上升到最高点,此过程运动距离为s2.
a2=gsinθ+μgcosθ=10m/s2,s1=$\frac{{v}_{1}^{2}-{v}^{2}}{2{a}_{2}}$=0.6m,s2=$\frac{{v}^{2}}{2{a}_{1}}$=1m,
因此与挡板P第一次碰撞后,木块B所达到的最高位置与挡板P的距离s=s1+s2=1.6m;
(2)经过多次碰撞后木块以2m/s的速度被反弹,在距N点1m的范围内不断以加速度a2做向上的减速运动和向下的加速运动,
木块对传送带有一与传送带运动方向相反的阻力:Ff=μmgcosθ,
故电动机的输出功率:P=μmgvcosθ=8W.
答:(1)木块与挡板P第一次碰撞后所达到的最高位置与挡板P的距离为1.6m.
(2)经过足够长时间后,电动机的输出功率保持不变,此输出功率大小为8W.
点评 本题是一个多过程问题,比较复杂,关键理清物块在传送带上整个过程中的运动规律,搞清摩擦力的方向,结合牛顿第二定律和运动学公式进行求解.

| A. | 由于液体表面层分子间距离小于液体内部分子间距离,液体表面存在张力 | |
| B. | 一块0℃的冰逐渐熔化成0℃的水,在这个过程中分子的平均动能不变 | |
| C. | 用油膜法测出油分子的直径后,要测定阿伏加德罗常数,只须再知道油的密度即可 | |
| D. | 甲、乙两个分子相距较远.若把甲固定,使乙分子逐渐向甲靠近,直到不能再靠拢为止,在这一过程中先是分子力对乙做正功,然后乙克服分子力做功 | |
| E. | 压缩气体,气体的内能可能减少 | |
| F. | 机械能无法全部转化为内能,内能也无法全部用来做功以转化为机械能 |
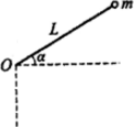 长为L的轻绳一端固定于O点,另一端系质量为m的小球,把小球拉离水平方向上方至绳与水平方向成α=30°时静止释放,当小球自由下落并摆至最低点时绳的张力F为(已知重力加速度为g)( )
长为L的轻绳一端固定于O点,另一端系质量为m的小球,把小球拉离水平方向上方至绳与水平方向成α=30°时静止释放,当小球自由下落并摆至最低点时绳的张力F为(已知重力加速度为g)( )| A. | 4mg | B. | 3.5mg | C. | 3mg | D. | 2.5mg |
 如图甲所示的电路中,理想变压器的原、副线圈匝数比为11:4,原线圈接入如图乙所示的电压,副线圈接火灾报警器系统(报警器未画出),电压表和电流表均为理想电表,R0为定值电阻,R为半导体热敏电阻,其阻值随温度的升高而减小,下列说法中正确的是( )
如图甲所示的电路中,理想变压器的原、副线圈匝数比为11:4,原线圈接入如图乙所示的电压,副线圈接火灾报警器系统(报警器未画出),电压表和电流表均为理想电表,R0为定值电阻,R为半导体热敏电阻,其阻值随温度的升高而减小,下列说法中正确的是( )| A. | 图乙中,电压的有效值为110$\sqrt{2}$V | |
| B. | 电压表的示数为40V | |
| C. | R处出现火警时,电流表示数减小 | |
| D. | R处出现火警时,电阻R0消耗的电功率增大 |
| 时刻/s | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 速度/m•s-1 | 3.0 | 6.0 | 9.0 | 12.0 | 15.0 | 18.0 |
| A. | 汽车运动的加速度大小为3m/s2 | B. | 汽车前6s内的位移大小为54m | ||
| C. | 汽车第8s末的速度大小为24m/s | D. | 汽车运动第7s内的位移大小为16m |
 如图是某物体v-t图象,其中t1时刻物体的速度为v1,t2时刻物体的速度为v2
如图是某物体v-t图象,其中t1时刻物体的速度为v1,t2时刻物体的速度为v2 如图所示,匀强磁场的磁感应强B=$\frac{\sqrt{2}}{π}$ T,边长L=10cm的正方形线圈abcd的匝数N=100匝,线圈总电阻r=1Ω,线圈绕垂直于磁感线的轴OO1匀速转动,角速度ω=2πrad/s,外电路电阻R=4Ω,电压表为理想电表.求:
如图所示,匀强磁场的磁感应强B=$\frac{\sqrt{2}}{π}$ T,边长L=10cm的正方形线圈abcd的匝数N=100匝,线圈总电阻r=1Ω,线圈绕垂直于磁感线的轴OO1匀速转动,角速度ω=2πrad/s,外电路电阻R=4Ω,电压表为理想电表.求: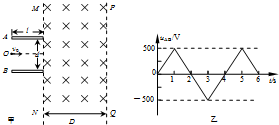 如图甲所示,两平行金属板A、B的板长l=0.20m,板间距d=0.20m,两金属板间加如图乙所示的交变电压,并在两板间形成交变的匀强电场,忽略其边缘效应.在金属板右侧有一方向垂直于纸面向里的匀强磁场,其左右宽度D=0.40m,上下范围足够大,边界MN和PQ均与金属板垂直.匀强磁场的磁感应强度B=1.0×10-2 T.现从t=0开始,从两极板左端的中点O处以每秒钟1000个的速率不停地释放出某种带正电的粒子,这些粒子均以vo=2.0×105m/s的速度沿两板间的中线射入电场,已知带电粒子的比荷$\frac{q}{m}$=1.0×108 C/kg,粒子的重力和粒子间的相互作用都忽略不计,在粒子通过电场区域的极短时间内极板间的电压可以看作不变.求:
如图甲所示,两平行金属板A、B的板长l=0.20m,板间距d=0.20m,两金属板间加如图乙所示的交变电压,并在两板间形成交变的匀强电场,忽略其边缘效应.在金属板右侧有一方向垂直于纸面向里的匀强磁场,其左右宽度D=0.40m,上下范围足够大,边界MN和PQ均与金属板垂直.匀强磁场的磁感应强度B=1.0×10-2 T.现从t=0开始,从两极板左端的中点O处以每秒钟1000个的速率不停地释放出某种带正电的粒子,这些粒子均以vo=2.0×105m/s的速度沿两板间的中线射入电场,已知带电粒子的比荷$\frac{q}{m}$=1.0×108 C/kg,粒子的重力和粒子间的相互作用都忽略不计,在粒子通过电场区域的极短时间内极板间的电压可以看作不变.求: