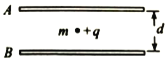Question

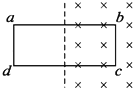
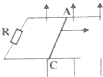
【题目】初速度可忽略的铁离子Fe2＋和Fe3＋，经电压为U的电场加速后，垂直进入磁感应强度大小为B、方向垂直纸面向里、有一定宽度的匀强磁场区域，如图所示．已知离子Fe2＋在磁场中转过θ＝30°后从磁场右边界射出．不计重力，在电场和磁场中运动时，离子Fe2＋和Fe3＋(　　)

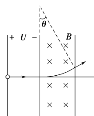
A. 在电场中的加速度之比为3∶2

B. 在磁场中运动的半径之比为：2

C. 在磁场中转过的角度之比为1∶2

D. 离开电场区域时的动能之比为2∶3

Answer 1

【答案】BD

【解析】

要分析加速度就要先分析其受的电场力，而要分析动能就要看电场做的功；要分析半径就要用洛伦兹力充当向心力，来找出半径，有了半径其转过的角度就很容易了。

两个离子的质量相同，其带电量是2：3的关系，所以由可知其在电场中的加速度是2：3，故A错误。要想知道半径必须先知道进入磁场的速度，而速度的决定因素是加速电场，所以在离开电场时其速度表达式为：，可知其速度之比为．又由qvB=m知，，所以其半径之比为：2，故B正确。由B的分析知道，离子在磁场中运动的半径之比为：2，设磁场宽度为L，离子通过磁场转过的角度等于其圆心角，所以有sinθ=L/R，则可知角度的正弦值之比为2：，又Fe2＋的角度为30°，可知Fe3+角度为，即在磁场中转过的角度之比不等于1：2，故C错误。由电场加速后：qU=mv2可知，两离子离开电场的动能之比为2：3，故D正确。故选BD。