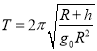��Ŀ����
����Ŀ����ͼ��ʾ��һ����ΪM��ƽ�峵B���ڹ⻬ˮƽ���ϣ�������˷�һ����Ϊm��Сľ��A������Ϊ�ʵ㣩��M>m��A��B��Ķ�Ħ������Ϊ������ƽ�峵�ҷ���ˮƽ���Ϲ̶�һ��ֱ����P����ʼʱA��B���ٶ�v0һ�������˶���ijʱ��B�뵲��P��ײ��������ԭ���ʷ��أ��ڴ˺���˶�������A���Ử��B���������ٶ�Ϊg����
��1��A��B�������ٶȣ�
��2��ľ�����С���ȣ�
��3��Сľ��A�뵲��P���ʱ��ƽ�峵B�����Ҷ˾൲��P�ľ��롣

���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
��������
(1)ѡˮƽ����Ϊ������Bײ�����AB��Ծ�ֹ��AB�����غ㣺
Mv0-mv0=(M+m)v����
��ã�
v��=![]()
(2)A��B����Ի����Ĺ���AB�����غ㣺
![]() (M+m)v02=
(M+m)v02=![]() (M+m)v��2+��mgL
(M+m)v��2+��mgL
��ã�
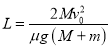
(3)Сľ��A�����ȼ��ٵ��ٶ�Ϊ��ʱA�뵲��P�����A��B�ϻ�����vA=0�Ĺ��̶����غ㣺
Mv0-mv0 =MvB
��ã�
vB=![]()
ƽ�峵B�����ȼ���ֱ�ߣ��ɶ��ܶ���֪��
-��mgx=![]() MvB2-
MvB2-![]() Mv02
Mv02
���
x=![]()

��ϰ��ϵ�д�
 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�
�����Ŀ