题目内容
|
如图所示,M、N是两个共轴圆筒的横截面,外筒半径为R,内筒半径比R小很多,可以忽略不计,筒的两端是封闭的,两筒之间抽成真空。两筒以相同的角速度 ω绕其中心轴线(图中垂直于纸面)做匀速转动。设从M筒内部可以通过窄缝 s(与M筒的轴线平行)连续向外射出速率分别为 v1和v2的粒子,粒子运动方向都沿筒的半径方向,粒子到达N筒后就附着在N筒上。如果R、v1和v2都不变,而ω取某一合适的值,则( ) 
|
ABC
解析两种粒子从窄缝 s射出后,沿半径方向匀速直线运动,到达N筒的时间分别为 和
和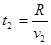 ,两种粒子到达N筒的时间差为
,两种粒子到达N筒的时间差为 ,N筒匀速转动,若在
,N筒匀速转动,若在 和
和 时间内转过的弧长均为周长的整数倍,则所有粒子均落在a处一条与 s缝平行的窄条上,A正确;若N筒在
时间内转过的弧长均为周长的整数倍,则所有粒子均落在a处一条与 s缝平行的窄条上,A正确;若N筒在 和
和 时间内转过的弧长不是周长的整数倍,但在
时间内转过的弧长不是周长的整数倍,但在 内转过的弧长恰为周长的整数倍,则所有粒子均落在如b处一条与 s缝平行的窄条上,B正确;若在
内转过的弧长恰为周长的整数倍,则所有粒子均落在如b处一条与 s缝平行的窄条上,B正确;若在 和
和 及
及 内转过的弧长均不是周长的整数倍,则可能落在N筒上某两处如 b处和c处与 s缝平行的窄条上,C正确;对应某一确定的ω值,N筒转过的弧长是一定的,故N筒上粒子到达的位置是一定的,D错误。
内转过的弧长均不是周长的整数倍,则可能落在N筒上某两处如 b处和c处与 s缝平行的窄条上,C正确;对应某一确定的ω值,N筒转过的弧长是一定的,故N筒上粒子到达的位置是一定的,D错误。
 和
和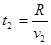 ,两种粒子到达N筒的时间差为
,两种粒子到达N筒的时间差为 ,N筒匀速转动,若在
,N筒匀速转动,若在 和
和 时间内转过的弧长均为周长的整数倍,则所有粒子均落在a处一条与 s缝平行的窄条上,A正确;若N筒在
时间内转过的弧长均为周长的整数倍,则所有粒子均落在a处一条与 s缝平行的窄条上,A正确;若N筒在 和
和 时间内转过的弧长不是周长的整数倍,但在
时间内转过的弧长不是周长的整数倍,但在 内转过的弧长恰为周长的整数倍,则所有粒子均落在如b处一条与 s缝平行的窄条上,B正确;若在
内转过的弧长恰为周长的整数倍,则所有粒子均落在如b处一条与 s缝平行的窄条上,B正确;若在 和
和 及
及 内转过的弧长均不是周长的整数倍,则可能落在N筒上某两处如 b处和c处与 s缝平行的窄条上,C正确;对应某一确定的ω值,N筒转过的弧长是一定的,故N筒上粒子到达的位置是一定的,D错误。
内转过的弧长均不是周长的整数倍,则可能落在N筒上某两处如 b处和c处与 s缝平行的窄条上,C正确;对应某一确定的ω值,N筒转过的弧长是一定的,故N筒上粒子到达的位置是一定的,D错误。
练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 E相切于D点,C为圆轨道的最低点,弧DC所对的圆心角θ=37o,半径R=1m。将质量m=0.5kg的物块置于轨道 ADC 上离地面高为 H处由静止释放,物体与斜面 AD 间的动摩擦因数μ=0.6,用力传感器测出其经过C点时对轨道的压力N,改变 H 的大小,可测出相应的 N 大小,试直接给出小物块到C点时对轨道的压力N随 H的关系式,并作出N随H的变化关系图。(不要求解题过程,重力加速度g取 10m/s2)。
E相切于D点,C为圆轨道的最低点,弧DC所对的圆心角θ=37o,半径R=1m。将质量m=0.5kg的物块置于轨道 ADC 上离地面高为 H处由静止释放,物体与斜面 AD 间的动摩擦因数μ=0.6,用力传感器测出其经过C点时对轨道的压力N,改变 H 的大小,可测出相应的 N 大小,试直接给出小物块到C点时对轨道的压力N随 H的关系式,并作出N随H的变化关系图。(不要求解题过程,重力加速度g取 10m/s2)。

 ,如图所示,则球对杆的作用力大小为( )
,如图所示,则球对杆的作用力大小为( )






 绕竖直轴高速转动,一颗子弹沿直径穿过圆桶,若子弹在圆桶转动不到半周过程中在圆桶上留下两个弹孔a、b,已知Oa与Ob间的夹角为θ,圆桶的直径为d,则子弹的速度为( )
绕竖直轴高速转动,一颗子弹沿直径穿过圆桶,若子弹在圆桶转动不到半周过程中在圆桶上留下两个弹孔a、b,已知Oa与Ob间的夹角为θ,圆桶的直径为d,则子弹的速度为( )