题目内容
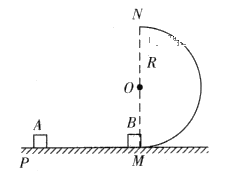
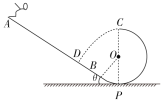
【题目】设一个质量m=50 kg的跳台花样滑雪运动员(可看成质点),从静止开始沿斜面雪道从A点滑下,沿切线从B点进入半径R=15 m的光滑竖直冰面圆轨道BPC,通过轨道最高点C水平飞出,经t =2 s落到斜面雪道上的D点,其速度方向与斜面垂直,斜面与水平面的夹角θ=37°,不计空气阻力,取当地的重力加速度g=10 m/s2,(sin37°=0.60,cos37°=0.80)。试求:
(1)运动员运动到C点时的速度大小vC;
(2)运动员在圆轨道最低点受到轨道支持力的大小FN。
(3)若A到P竖直高度H=45m,则A到P过程克服摩擦力做功多少?
【答案】(1)15 m/s (2)3250 N (3)1875 J
【解析】
(1)在D点,由平抛运动,分解速度得 :vy=gt =20 m/s
tan37°=![]()
解得:vC=15 m/s
(2)对P到C过程,由动能定理得:
![]()
在P点,根据牛顿第二定律:
![]()
解得:FN=3250 N
(3)A到P过程,设克服摩擦力做功为Wf,由动能定理得:
![]()
解得:Wf =1875 J

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目