��Ŀ����
����Ŀ����ͼ��ʾ��x����ˮƽ���ʹ��غϣ�����ԭ��O�ڴ��ʹ�����ˣ����ʹ���L��8m�����ʹ��Ҷ�Q�����ֱ�⻬Բ�����Բ����ͬһ��ֱ���ϣ�Ƥ�������˶����ٶ�v0��5m/s��һ����m��1kg��С���������ڴ��ʹ���xP��2m��P�㣬С����洫�ʹ��˶���Q���ǡ���ܳ��Ϲ⻬Բ���������ߵ�N�㡣С����봫�ʹ���Ķ�Ħ����������0.5���������ٶ�g��10 m/s2����
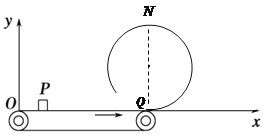
��1��N��������ꣻ
��2����P�㵽Q�㣬С����ڴ��ʹ����˶�ϵͳ������������
��3������С�������ڴ��ʹ��ϵ�ijЩλ�ã�С�������ع⻬Բ������˶���С���ʼ����Բ������˶����ѹ죩����������yM=0.25m��M�㣬����Щλ�õĺ����귶Χ��
���𰸡���1��yN=1m����2��7m��x��7 .5m��0��x��5 .5m
��������
����������P��Q���̵ļ��ٶȣ��ڸ����˶�ѧ��ʽ��ʽ����Q����ٶȣ���N�㣬����ǡ���ṩ������������ţ�ٵڶ����ɺ�����Բ���˶���ʽ������뾶�����Ħ���������λ�ƿɸ���Q=f��S���������������ܵ���N��ʱ���������������ܵ���ĸ߶ȳ����뾶��û����N����������������ܵ���߶Ȳ������뾶�����������ɸ��������غ������Ӧ��λ�ƣ��Ӷ�������ꣻ
С����ڴ��ʹ��ϵļ��ٶ�![]()
С����봫�ʹ�����ʱ�����õ�ʱ��![]()
�˶���λ��![]()
����![]()
�ɻ�е���غ㶨�ɵ�![]() �����
�����![]()
��2��С����ڴ��ʹ�����Դ��ʹ�������λ��
![]()
����������![]()
��3����������Ϊx1����С�������ڴ��ʹ��ϣ������ܵ���Բ���Ҳ��M�㣬�������غ�ã�
��mg(L��x1)��mgyM
�������ݽ��x1��7.5 m
��mg(L��x2)��mgyN
�������ݽ��x2��7 m
�����ܵ���Բ������M�㣬��(1)��֪x3��5.5 m







