题目内容
【题目】图示为一小球做平抛运动的频闪照片的一部分。图中背景最小方格的边长均为L;重力加速度为g则:
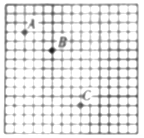
(1)小球从A运动到C的时间可表示为_______
(2)小球做平抛运动的初速度可表示为________;
(3)若以抛出点为坐标原点,水平向右为x轴正方向,竖直向下为y轴正方向,则C点的坐标可表示为____;
【答案】![]()
![]() (6l,8l)
(6l,8l)
【解析】
(1)依据平抛运动的水平方向做匀速直线运动,从图中可以看出:A、B、C3个点间的水平位移均相等为3L,因此这3个点是等时间间隔点,根据竖直方向做自由落体运动,则有![]() ,求解;
,求解;
(2) 依据平抛运动的水平方向做匀速直线运动,那么![]() ,即可解出;
,即可解出;
(3) 根据中间时刻的瞬时速度等于此段位移的平均速度,可得小球到达B点的速度,于是可得小球从抛出到B的时间,从而可求得C点的速度,再通过C点竖直分速度求出平抛运动的时间,从而根据水平方向和竖直方向上的运动规律求出C点对的坐标。
(1) 从图中看出,A、B、C、3个点间的水平位移均相等,是x=3l
因此这3个点是等时间间隔点
竖直方向两段相邻位移之差是个定值
即△y=gT2=4l,
解得:![]()
因此小球从A运动到C的时间可表示为:![]()
(2)再根据水平方向有:
3l=v0T
得:![]() ;
;
(3) 根据中间时刻的瞬时速度等于此段位移的平均速度,可得小球到达B点的竖直方向分速度为:![]()
那么小球到达C点的竖直方向分速度为:![]()
因此从抛出点到C点的时间为t=![]()
那么C点的竖直位移为:![]()
而水平位移为:![]()
因此C点的坐标为(6l,8l)。

练习册系列答案
相关题目