Question

【题目】如图所示，以O为圆心、半径为R的圆形区域内存在垂直圆面向里、磁感应强度为B的匀强磁场，一粒子源位于圆周上的M点，可向磁场区域内垂直磁场沿各个方向发射质量为m、电荷量为－q的粒子，不计粒子重力，N为圆周上另一点，半径OM和ON间的夹角θ，且满足tan＝0.5.

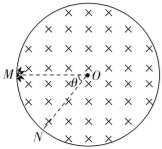
(1)若某一粒子以速率v1＝沿与MO成60°角斜向上方向射入磁场，求此粒子在磁场中运动的时间；

(2)若某一粒子以速率v2沿MO方向射入磁场，恰能从N点离开磁场，求此粒子的速率v2；

(3)若由M点射入磁场各个方向的所有粒子速率均为v2，求磁场中有粒子通过的区域面积．

Answer 1

【答案】 (1) (2) (3) πR2－R2

【解析】(1)粒子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，设轨迹半径为r1，由牛顿第二定律可得qv1B＝，解得r1＝＝R.

粒子沿与MO成60°角的方向射入磁场，设粒子从区域边界P点射出，其运动轨迹如图所示．由图中几何关系可知粒子轨迹所对应的圆心角为α＝150°.

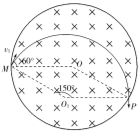
法二：粒子运动周期T＝，

粒子在磁场中的运动的时间t＝T，解得t＝.

(2)粒子以速率v2沿MO方向射入磁场，在磁场中做匀速圆周运动，恰好从N点离开磁场，其运动轨迹如图所示，设粒子轨迹半径为r2，由图中几何关系可得

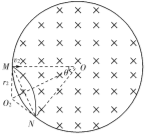
r2＝Rtan＝R，

由牛顿第二定律可得

qv2B＝，

解得v2＝.

(3)粒子沿各个方向以v2进入磁场做匀速圆周运动时的轨迹半径都为r2，且不变．由图可知，粒子在磁场中通过的面积S等于以O3为圆心的半圆的面积S1、以M为圆心的扇形MOQ的面积S2和以O点为圆心的圆弧MQ与直线MQ围成的面积S3之和．

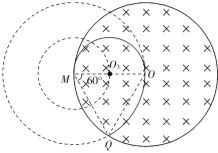
S1＝π＝πR2，S2＝πR2，

S3＝πR2－R2，

则S＝S1＋S2＋S3＝πR2－R2