题目内容
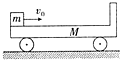 (2012?泗县模拟)如图所示,质量为M,长为L的小车静止在光滑水平面上,小车最右端有一个厚度不计的竖直挡板,另有一质量为m的小物体以水平向右的初速度v0从小车最左端出发,运动过程中与小车右端的挡板发生无机械能损失的碰撞,碰后小物体恰好停在小车的正中位置.
(2012?泗县模拟)如图所示,质量为M,长为L的小车静止在光滑水平面上,小车最右端有一个厚度不计的竖直挡板,另有一质量为m的小物体以水平向右的初速度v0从小车最左端出发,运动过程中与小车右端的挡板发生无机械能损失的碰撞,碰后小物体恰好停在小车的正中位置.求:(1)小物体与小车间的动摩擦因数.
(2)碰撞前小车的加速度.
分析:(1)系统动量守恒,应用动量守恒时不用关注复杂的相互运动过程,只看初末状态即可,系统损失的动能等于系统克服摩擦力做功,即系统产生的内能,因此根据动量守恒和功能关系列方程即可解出结果.
(2)碰撞前小车受到小物体给其水平向右的摩擦力,根据牛顿第二定律列方程即可求出结果.
(2)碰撞前小车受到小物体给其水平向右的摩擦力,根据牛顿第二定律列方程即可求出结果.
解答:解:(1)设最后二者共同速度为v,由动量守恒定律:
mv0=(M+m)v ①
对系统由功能关系得:
μmg(L+
) =
m
-
(M+m)v2 ②
联立①②可得:μ=
③
所以小物体与小车间的动摩擦因数为μ=
(2)对小车由牛顿第二定律可得:
μmg=Ma ④
联立③④可得:a=
所以碰撞前小车的加速度为a=
.
mv0=(M+m)v ①
对系统由功能关系得:
μmg(L+
| L |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
联立①②可得:μ=
M
| ||
| 3(m+M)gL |
所以小物体与小车间的动摩擦因数为μ=
M
| ||
| 3(m+M)gL |
(2)对小车由牛顿第二定律可得:
μmg=Ma ④
联立③④可得:a=
m
| ||
| 3(m+M)L |
所以碰撞前小车的加速度为a=
m
| ||
| 3(m+M)L |
点评:正确应用动量守恒和功能关系列方程是解决这类问题的关键,尤其是弄清相互作用过程中的功能关系.

练习册系列答案
相关题目
 (2012?泗县模拟)如图所示,在同一轨道平面上的几个人造星球卫星A、B、C,在某一时刻恰好在同一条直线上,下列说法中正确的是( )
(2012?泗县模拟)如图所示,在同一轨道平面上的几个人造星球卫星A、B、C,在某一时刻恰好在同一条直线上,下列说法中正确的是( )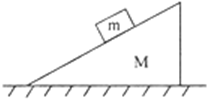 (2012?泗县模拟)质量为m的物体,沿质量为M的固定斜面匀速下滑,如图,斜面的倾角为θ,则下列说法正确的是( )
(2012?泗县模拟)质量为m的物体,沿质量为M的固定斜面匀速下滑,如图,斜面的倾角为θ,则下列说法正确的是( )