题目内容
如图所示，在x＞0、y＞0空间存在一恒定的匀强磁场，磁感应强度的方向垂直于xOy平面向里，大小为B．现把α粒子（4 2 |
1 1 |
分析：两种粒子均做匀速圆周运动，根据几何关系得到半径之比，然后根据洛伦兹力提供向心力列式分析判断．
解答：解：A、B、根据洛伦兹力提供向心力，有qvB=m
，解得R=
；
故α粒子与质子在磁场中作圆周运动的半径之比为
=
?
=
×
=
，故A错误，B错误；
C、由几何关系，两段圆弧的半径之比为2：1，故圆弧长度之比为：Sα：SH=Rα?
：RH?π=1：1，即两段圆弧的长度相等，故C错误；
D、周期T=
=
；
由于tα=
Tα，tH=
TH，
故tα：tH=
Tα：
TH=1：1，故D正确；
故选D．
| v2 |
| R |
| mv |
| qB |
故α粒子与质子在磁场中作圆周运动的半径之比为
| rα |
| rH |
| mα |
| mH |
| qH |
| qα |
| 4 |
| 1 |
| 1 |
| 2 |
| 2 |
| 1 |
C、由几何关系，两段圆弧的半径之比为2：1，故圆弧长度之比为：Sα：SH=Rα?
| π |
| 2 |
D、周期T=
| 2πr |
| v |
| 2πm |
| qB |
由于tα=
| 1 |
| 4 |
| 1 |
| 2 |
故tα：tH=
| 90° |
| 360° |
| 180° |
| 360° |
故选D．
点评：本题关键根据洛伦兹力提供向心力求解出半径和周期表达式，再根据几何关系得到半径之比，然后列式分析．
练习册系列答案
相关题目
如图所示，在x＞0、y＞0（第Ⅰ象限）的空间存在沿y轴负方向的匀强电场，场强大小为E，一个粒子源发射相同的带正电粒子，粒子的初速度恒定，并从y轴上的P（0，2L）点沿x轴正方向射入匀强电场中，粒子经电场作用后恰好从x轴上的Q（L，0）点射出．若撤去电场，在此区域加一方向垂直于xoy平面的匀强磁场，磁感强度大小为B，其它条件不变，粒子仍恰好从Q射出，不计粒子的重力和粒子之间的相互作用，（取：
如图所示，在x＞0，y＞0的空间中有一匀强磁场，磁感应强度的方向垂直于xOy平面向里，大小为B．现有一质量为m、电量为q的带正电粒子，从在x轴上的某点P沿着与x轴成30°角的方向射入磁场．不计重力的影响，则下列有关说法中正确的是（ ）
如图所示，在x＞0、y＞0的空间中有恒定的匀强磁场，磁感应强度的方向垂直于xOy平面向里，大小为B．现有一质量为m、电量为q的带电粒子，在x轴上到原点的距离为x0的P点，以平行于y轴的初速度射入磁场．在磁场作用下沿垂直于y轴的方向射出磁场．不计重力的影响，由这些信息可以确定的是（ ）
如图所示，在x＜0且y＜0的区域内存在垂直纸面向里的匀强磁场，磁感应强度大小为B，在x＞0且y＜0的区域内存在沿y轴正方向的匀强电场．一质量为m、电荷量为q的带电粒子从x轴上的M点沿y轴负方向垂直射入磁场，结果带电粒子从y轴的N点射出磁场而进入匀强电场，经电场偏转后打到x轴上的P点，已知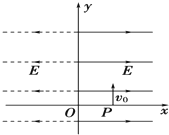
如图所示，在x＞0的空间内存在沿x轴正方向的匀强电场，电场强度为E；在x＜0的空间内存在沿x轴负方向的匀强电场，场强大小也等于E．一电子（-e，m）在x=d处的P点以沿y轴正方向的初速度v0开始运动，不计电子重力．求：